$1.3.13^*.$ From a hose lying on the ground, water shoots at an angle of $45^\circ$ to the horizon with an initial velocity of $10$ $\frac{m}{s}$. The cross-sectional area of the hose opening is $5$ $cm^2$ . Determine the mass of the jet in the air.
a) We will use the formula for the flight path obtained in 1.3.6:
$$ y(x) = x \tan \varphi-\frac{gx^2}{2v^2\cos^2\varphi} $$Let's use the hint,
$$ y(x) = x \tan \varphi-\frac{gx^2}{2v^2}(1+\tan ^2 \varphi)\;(1) $$Where do we express the angle $ \varphi$:
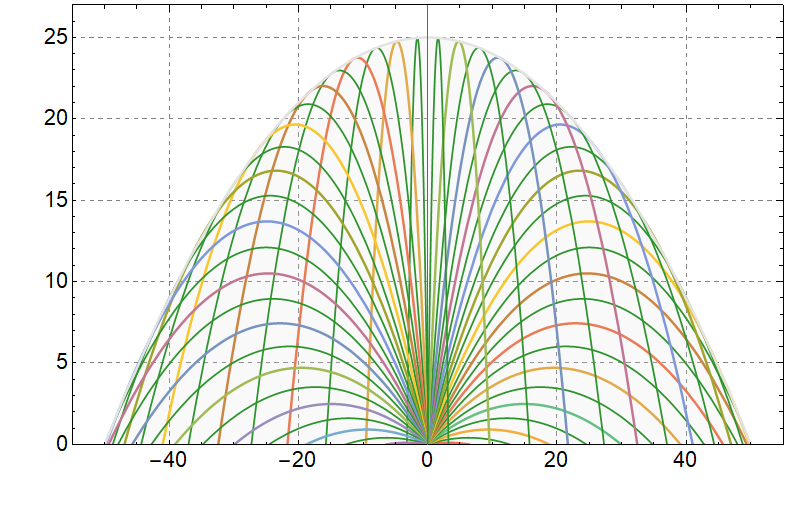
$$ \tan \varphi=\frac{v^2\pm\sqrt{v^4-2gv^2y-g^2x^2}}{gx} $$b) Let's depict a set of trajectories, changing the angle $\varphi$ from $-\frac{\pi}{2}$ to $\frac{\pi}{2}$:

Having analyzed the domain of definition of the function $(1)$, we emphasize that the expression under the root is not negative
$$ v^4-2gv^2y-g^2x^2 \geq 0 $$ $$ y \leq \frac{v^2}{2g}-\frac{gx^2}{2v^2} $$c) From $(1)$, we get:
$$ v_{x}v_{y}x-\frac{1}{2}gx^{2}=v_{x}^{2}y $$We will use the formula for horizontal and vertical coordinates obtained in 1.3.6:
$$ y(t) = vt \cdot \sin{\varphi} - \frac{gt^2}{2} $$ $$ x(t) = vt \cdot \cos{\varphi} $$Let $\xi=\cos{\varphi}$,
$$ v_y = v \xi $$ $$ v_x = v \sqrt{1-\xi ^2} $$Getting a function
$$ v(\xi)=\frac{\sqrt{g}x}{\sqrt{2 \xi \sqrt{1-\xi ^{2}}x-\xi ^{2}y}} \;(2) $$The maximum of the radical value corresponds to the minimum of the function (2)
$$ (\sqrt{x^{2}+y^{2}-y})/2 \rightarrow \max $$Minimum of function $(2)$
$$ \fbox{$v^{2}=\frac{gx}{\sqrt{1+(\frac{y}{x})^{2}}-\frac{y}{x}}$} $$$$\tan \varphi=\frac{v^2\pm\sqrt{v^4-2gv^2y-g^2x^2}}{gx}.$$ $$y=\frac{v^2}{2g}-\frac{gx^2}{2v^2}$$ $$v_{\text{min}}=\sqrt{g(y+\sqrt{x^2+y^2})}$$