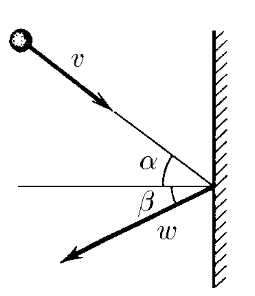
$1.4.9.$ The body hits the wall with velocity $v$ and angle $\alpha$ to the line perpendicular to the wall. Determine the velocity of the body after an elastic impact if the wall is:
a) stationary;
b) moving perpendicular to itself at a speed $w$ towards the body;
c) moving at an angle $\beta$ to the line perpendicular to it at a speed $w$ towards the body.

$a)$ Since the collision is elastic, then according to the Law of Conservation of Momentum:
$$v \sin \alpha = u \sin \alpha $$ $$\fbox{$v = u $}$$$б)$ Further, this problem is a little reminiscent of 1.4.8.
In the frame of reference associated with the wall, the relative velocity of the ball $\vec{v_{rel}} = \vec{v} - \vec{w}$. During elastic reflection, passing into the earth's frame of reference, the velocity is equal to $\vec{u} = \vec{v} - 2\vec{w}$.
Working with vector quantities is clearly demonstrated below
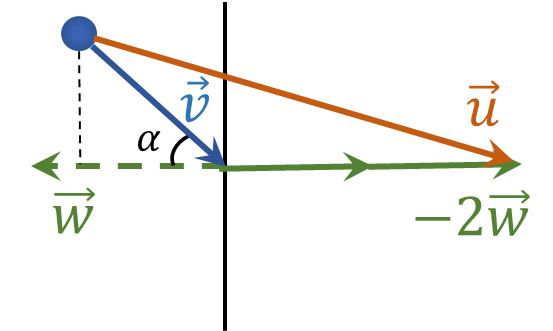
Let's find the projections of the vector $\vec{u}$ on the horizontal and vertical axes:
$$u_y = v \sin \alpha $$ $$u_x = v \cos \alpha + 2w$$Using the Pythagorean theorem, we find the modulus of the vector $\vec{u}$
$$u = \sqrt{u_x^2+u_y^2}$$ $$u = \sqrt{(v \sin \alpha)^2 + (v \cos \alpha + 2w)^2}$$ $$\fbox{$u=\sqrt{v^{2}+4vw\cos\alpha+4w^{2}}$}$$$в)$ Similar to the previous subparagraph
$$\vec{u} = \vec{v} - 2\vec{w}$$We will show these vectors in the figure
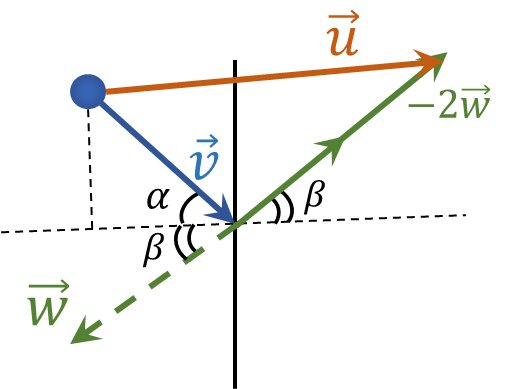
We will find the projections of the vector $\vec{u}$ on the horizontal and vertical axis:
$$u_y = v \sin \alpha - 2w \sin \beta$$ $$u_x = v \cos \alpha + 2w \cos \beta$$Using the Pythagorean equation, we find the modulus of the vector $\vec{u}$ $$u = \sqrt{u_x^2+u_y^2}$$ $$u = \sqrt{(v \sin \alpha - 2w \sin \beta)^2 + (v \cos \alpha + 2w \cos \beta)^2}$$ $$\fbox{$u=\sqrt{v^{2}+4vw\cos\alpha\cos\beta+4w^{2}\cos^{2}\beta}$}$$
$\text{a) } u=v.\quad\text{b) } u=\sqrt{v^{2}+4vw\cos\alpha+4w^{2}}.\quad\text{c) } u=\sqrt{v^{2}+4vw\cos\alpha\cos\beta+4w^{2}\cos^{2}\beta}.$