$13.2.14.$ a. A light beam passes through a wedge with a small angle $\alpha$ at the vertex,
which is perpendicular to the front face of the wedge. Prove that the angle
of deflection of the ray from the initial direction is approximately $(n − 1) \alpha$.
Refractive index of the wedge $n$.
b. A light ray passes through a wedge with a small angle $\alpha$ at the vertex,
which falls at a small angle $\gamma$ to the normal to the front surface of the wedge.
Prove that the angle of deflection of the light beam from the initial direction
is approximately $(n − 1) \alpha$. Refractive index of the wedge $n$.
c. Print the formula for the focal length of a thin lens. The radii of curvature
of the lens surface are $R_1$ and $R_2$, and the refractive index of the lens material
is $n$.
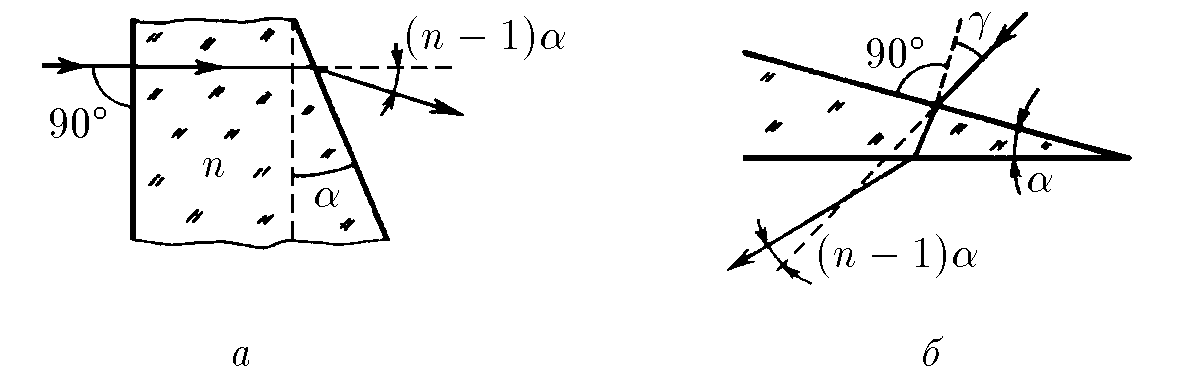
Let's imagine there is a parallel lays of light entering the lens with refractive index $n_1$ from media with refractive index $n_0$, and after lens there is a media with refractive index $n_2$.
First, let's consider the moment when ray hits front of lens at the point $h$ above optical axis.
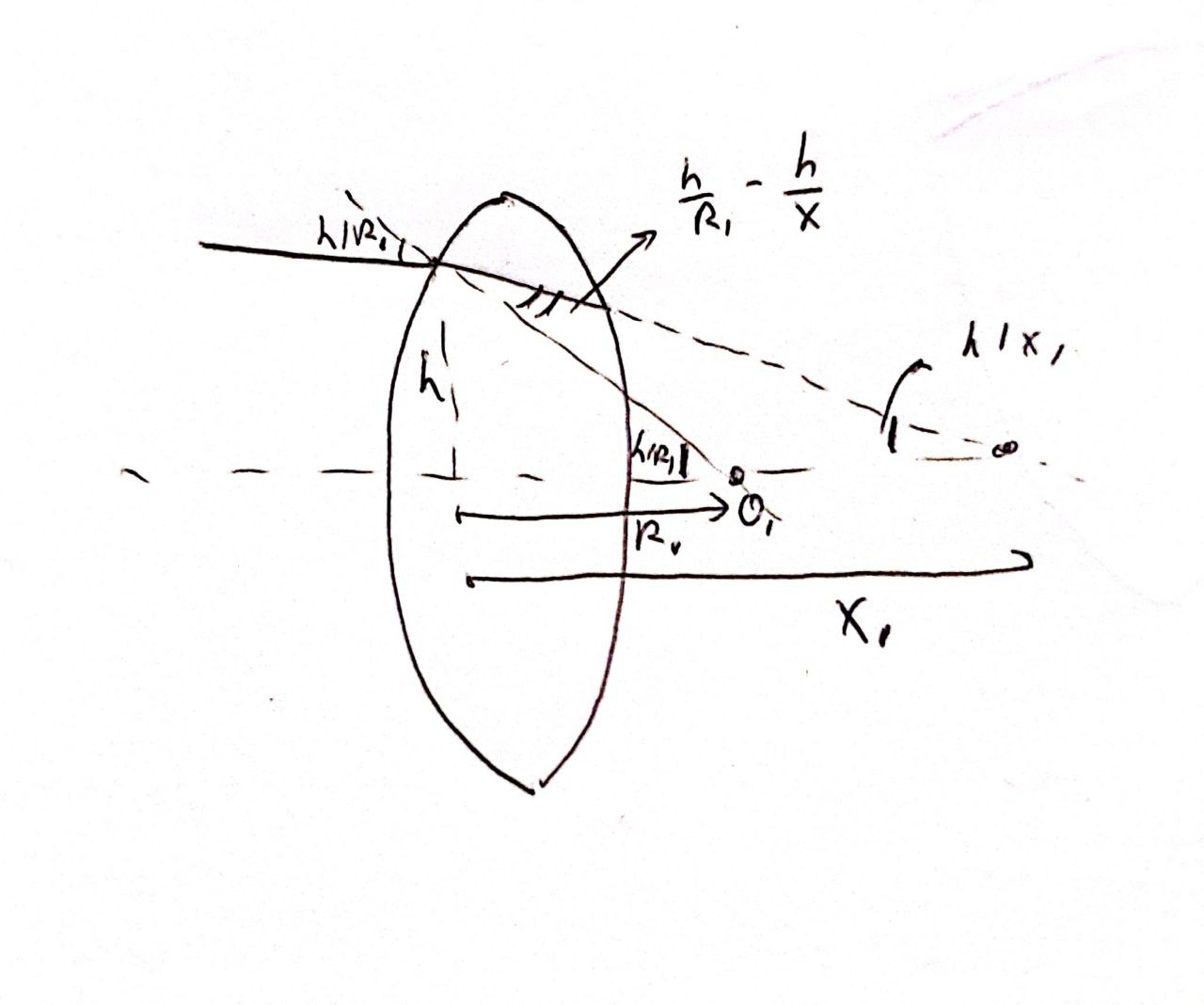
As shown in the picture, the incidence angle is $$\tan(\alpha) \approx \frac{h}{R_1} \approx sin{(\alpha)} \approx \alpha$$
where $R_1$ is the curvature radius of first surface.
If there wasn't second surface, the ray after refraction will cross the optical axis at point $x_1$, and angle is $\tan(b) \approx \sin(\beta) \approx \beta = x_1/h$. So, the refraction angle is
$$ \alpha - \beta = \frac{h}{R_1} - \frac{h}{x_1}$$
And by Snell's law:
$$n_0 \cdot \frac{h}{R_1} = n_1 \cdot \left(\frac{h}{R_1} - \frac{h}{R_2}\right)$$
After hitting the second surface, the ray will cross the axis at point $x_2$, which we want to find.
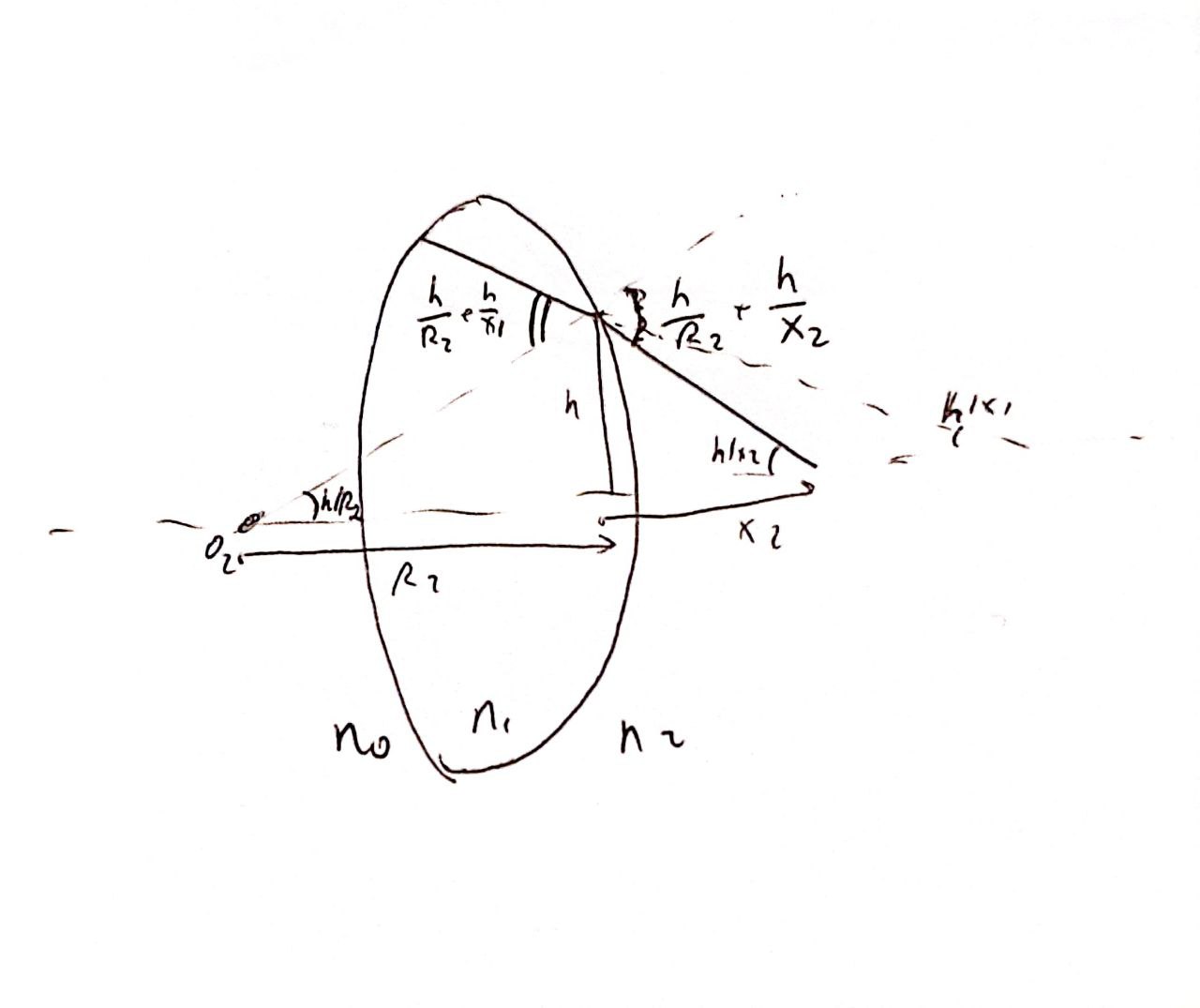
The incidence angle is
$$
\alpha_2 = \frac{h}{R_2} + \frac{h}{x_1}
$$
And the refraction angle is
$$
\beta_2 = \frac{h}{R_2} + \frac{h}{x_2}
$$
By Snell's Law:
$$
n_1 \cdot \alpha_2 = n_2 \cdot \beta_2
$$
Therefore:
$$
n_1 \cdot \left(\frac{h}{R_2} + \frac{h}{x_1} \right) = n_2 \cdot \left(\frac{h}{R_2} + \frac{h}{x_2} \right)
$$
So, we have a system of equations:
$$\begin{cases}
n_0 \cdot \frac{h}{R_1} = n_1 \cdot \left(\frac{h}{R_1} - \frac{h}{R_2}\right)\
n_1 \cdot \left(\frac{h}{R_2} + \frac{h}{x_1} \right) = n_2 \cdot \left(\frac{h}{R_2} + \frac{h}{x_2} \right)
\end{cases}
$$
Solving it, we can find $\frac{1}{x_2}$:
$$
\frac{1}{x_2} = \left(\frac{n_1}{n_2} -1 \right) \cdot \frac{1}{R_2} + \left(\frac{n_1}{n_2} - \frac{n_0}{n_2} \right) \cdot \frac{1}{R_1} = \frac{1}{F}
$$
In this problem, we have $n_0 = n_2 = 1, n_1 = n$
So, we have
$$
\boxed{\frac{1}{F} = \left(n-1 \right) \cdot \left(\frac{1}{R_1} + \frac{1}{R_2} \right)}
$$
$$\frac{1}{F}=(n-1)\left(\frac{1}{R_1}+\frac{1}{R_2}\right)$$
The solution was kindly provided by David Hayrapetyan