$2.1.35^*.$ The mass of the balloon together with the rope dragging along the ground is $m$; the buoyant force acting on the balloon is $F$; the coefficient of friction of the rope on the ground is $\mu$. The air resistance force acting on the balloon is proportional to the square of the balloon's velocity relative to the air: $f = \alpha v^2$. Find the velocity of the balloon relative to the ground if a horizontal wind is blowing with a velocity of $u$.

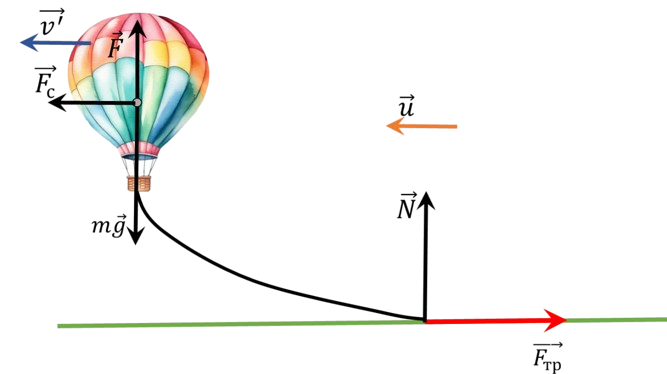
There are five forces acting on the balloon (see fig.): gravity $\vec{F}_{т} = M \vec{g}$, buoyancy $\vec{F}$, air resistance $\vec{F}_{c}$, Earth reaction force $\vec{N}$ and Earth friction force $\vec{F}_{пт}$.
Let $\vec{v}^{ \prime}$ denote the velocity of the balloon relative to the Earth. Then $$ \vec{F}_{c} = - \alpha ( \vec{v}^{ \prime} - \vec{u}) $$ From the condition that the balloon moves uniformly in the horizontal direction, it follows $$ | \vec{F}_{c} | - | \vec{F}_{тр} | = 0 $$ $$ | \vec{F}| + | \vec{N}| - M | \vec{g} | = 0 $$ Besides, $$ | \vec{F}_{тр} | = \mu | \vec{N} | $$ Taking into account that $$ | \vec{F}_{c}| = - \alpha ( | \vec{v}^{ \prime} | - | \vec{u} | ) $$ from the last three equations we get $$ | \vec{v}^{ \prime} | = | \vec{u} | - \frac{ \mu}{ \alpha} (M | \vec{g} | - | \vec{F} | ) $$
$v = u − \sqrt{(\mu /\alpha )(mg − F)}$ at $\alpha u^2 \geq \mu (mg − F)$, otherwise $v = 0$