$2.1.41.$ Which washer, rotating around its axis or not rotating, will go the longest way to stop on a rough horizontal surface? The initial velocity of the puck centers is the same.
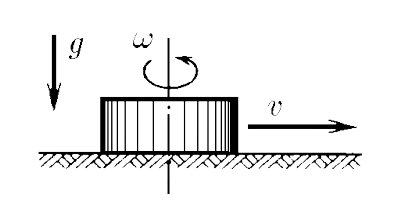
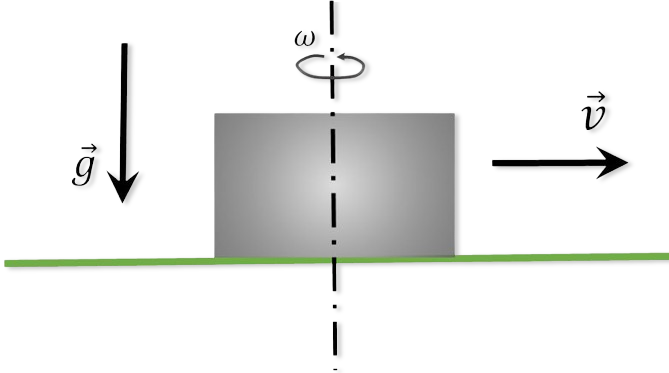
1. A reciprocating puck has only the kinetic energy of reciprocating motion $$ K_1=\frac{mv^2}{2} $$ the flat motion of the puck, which is a superposition of translational and rotational motion, is characterized by two components of kinetic energy: translational and rotational: $$ K_2=\frac{mv^2}{2}+J_z\frac{\omega^2}{2} $$ $$ K_2=\frac{mv^2}{2}+\frac{mr^2}{2}\cdot\frac{\omega^2}{2} $$ $$ K_2=\frac{m}{2}(v^2+\frac{r^2 \omega^2}{2}) $$ $$ K_2=\frac{3}{4}mv^2 $$ $$ K_2>K_1 $$ 2. The initial kinetic energy of the washers in both cases will be spent on work against the friction force. $$ A_{тр} = \mu mg\Delta x $$ 3. According to the theorem on the change in kinetic energy: $$ \frac{K_2}{K_1}=\frac{\Delta x_2}{\Delta x_1}=1.5 $$
Rotating