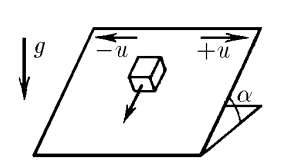
$2.1.44^*.$ Determine the steady-state velocity of a body on an inclined plane that changes one direction of its velocity $u$ to the opposite direction with high frequency. The direction of movement of the plane is shown in the figure. Coefficient of friction $\mu$, angle of inclination of the plane $\alpha$, $\tan\alpha < \mu$.
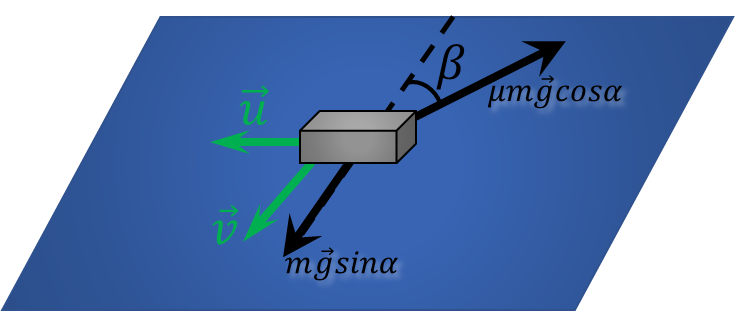
Since the speed changes quickly, the body does not have time to move in the horizontal direction and all the time moves in the direction of $\vec{v}$
Since $v=\text{const}$, there is no acceleration in the direction along the speed $\vec{v}$ $$ mg\sin\alpha = \mu mg \cos\alpha\cos\beta$$ $$ \cos\beta = \frac{\tan\alpha}{\mu} $$ From geometric considerations, the moduli of the vectors $\vec{v}$ and $\vec{u}$ are related by the relation $$ v=\frac{u}{\tan\beta} $$ $$ v=u \frac{\frac{\tan\alpha}{\mu}}{\sqrt{1-\frac{\tan^2\alpha}{\mu^2}}} $$ $$ \boxed{v = u \frac{\tan\alpha}{\sqrt{\mu^{2} − \tan^{2} \alpha}}} $$
$$v = u \frac{\, \text{tg} \alpha}{\sqrt{\mu^{2} − \text{tg}^{2} \alpha}}$$