$2.1.48.$ A wedge of mass $m_2$ with an angle $\alpha$ is inserted between two identical smooth bars of mass $m_1$. Determine the acceleration of bodies.
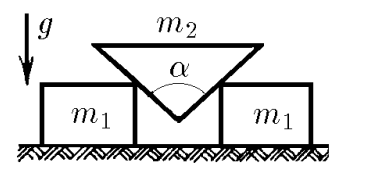
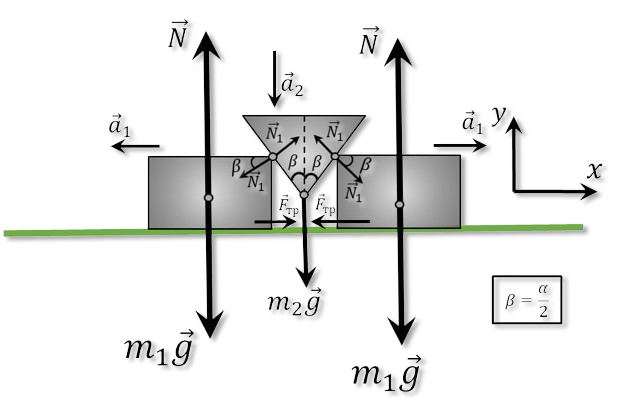
Let us consider a small displacement over time $dt$ from the point of view of kinematics:
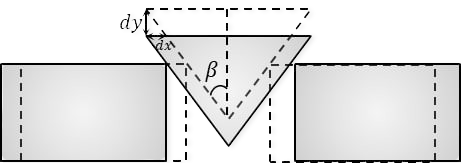
From geometric considerations: $$ dy = dx \cdot c\tan\beta$$ Let us differentiate both parts of the expression twice: $$ \frac{dy}{d^2t} = \frac{dx}{d^2t} \cdot c\tan\beta$$ $$ a_1 = a_2 \cdot \tan\beta\quad(1) $$ Since the Author did not say anything about friction, example $F_{tr}=0$ Next, we write Newton's 2nd law for the bar $m_1$ on the $OY$ axis: $$ m_1a_1=N_1\cos\beta$$ $$ N_1=\frac{m_1a_1}{\cos\beta}\quad(a) $$ Similarly for $m_2$: $$ m_2a_2=m_2g-2N_1\,\sin\beta\quad(b) $$ Substitute $(a)$ into $(b)$: $$ m_2a_2=m_2g-2m_1a_1\cdot \tan\beta$$ We substitute $(1)$ into $(c)$: $$ m_2a_2=m_2g-2m_1a_2\cdot \tan^2\beta$$ We express $a_2$: $$ \boxed{a_2=\frac{m_2g}{m_2+2m_1\,\tan^2\beta}}\quad(d) $$ Given $(1)$, we multiply $(d)$ by $\tan\beta$: $$ \boxed{a_1=\frac{m_2g\,\tan\beta}{m_2+2m_1\,\tan^2\beta}} $$
$$a_1=\frac{m_2g\,\tan\beta}{m_2+2m_1\,\tan^2\beta}$$ $$a_2=\frac{m_2g}{m_2+2m_1\,\tan^2\beta}$$