$2.4.34$ Two loads of mass $m_1$ and $m_2$ ($m_1 > m_2$) are connected by a thread thrown over a fixed block. At the initial moment, the load of mass $m_1$ is held at a height $h$ above the floor. Then it is released without a push. How much heat will be released when the load hits the floor? The impact is absolutely inelastic.
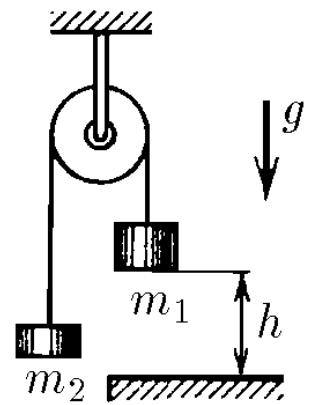
Applying Energy Conservation Law: $$m_1 g h = Q + m_2 g H\;(1)$$ where $Q$ is lost energy by heat and $H$ is the height achieved by body of mass $m_2$ after the impact of body of mass $m_1$, and is given by, $$H = h + \frac{v^2}{2g}\;(2)$$ Why? Potential energy of body 1 is converted in kinetic energy of body 1 and kinetic energy of body 2 with same velocity due to the constraint ($v_1=v_2=v$), after totally inelastic collision with ground, part of this energy is transformed in heat and the other one in potential energy for body 2, which behaves as a projectile launched vertically upwards from height $h$. For determining this velocity $v$, it's necessary to know what acceleration did the system have before impact. Applying Newton Second Law, for body 1: $$m_1 g - T = m_1 a \;(3)$$ and for body 2, $$T - m_2 g = m_2 a\;(4)$$ Suming up equations (3) and (4) side by side, $$a = \frac{m_1-m_2}{m_1+m_2}g\;(5)$$ As $h = \frac{v^2}{2a}$, so, $$v = \sqrt{2ah}\;(6)$$ Substituting (5) into (6), $$v = \sqrt{2gh\left(\frac{m_1-m_2}{m_1+m_2}\right)}\;(7)$$ Putting (7) into (2) $$H = \frac{2m_1}{m_1+m_2}h\;(8)$$ Finally, substituting (8) into (1) and separating $Q$,
$$Q = m_1gh \frac{m_1-m_2}{m_1+m_2}$$