$2.5.36.$ A bullet of mass $m_1$ having an initial velocity $v$ penetrates a lead ball of mass $m_2$ suspended on a thread and flies out of it at half speed. How much of the bullet's kinetic energy was converted to heat?
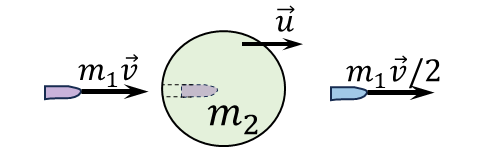
After the collision, the velocity of the lead ball $u$ could be found from the preservation of momentum $$m_1 v = m_2 u + \frac{m_1v}{2}$$ From here the velocity of the lead ball $u$ is $$u = v \frac{m_1}{2m_2}$$ Considering the energy $Q$ converted to heat, the conservation of energy could be written as $$\frac{m_1v^2}{2} = \frac{m_1(v/2)^2}{2} + \frac{m_2u^2}{2} + Q \quad(1)$$ Where the initial kinetic energy $$E_K = \frac{m_1v^2}{2}\quad(2)$$ From $(1)$, the amount of heat released $$Q = \frac{m_1v^2}{8} + \frac{m_1^2v^2}{2m_2} - \frac{m_1v^2}{2}\quad(3)$$ Deviding $(2)$ and $(3)$ equations, we obtain $$\boxed{\frac{E_K}{Q} = \frac{3- {m_1}/{m_2}}{4}}$$
$$Q/K=(3-m_1/m_2)/4$$