$2.7.20^*.$ A spool of thread lies on a horizontal plane. The reel is pulled by a thread. At what angles $\alpha$ between the force and the horizontal will the coil accelerate towards the taut thread?
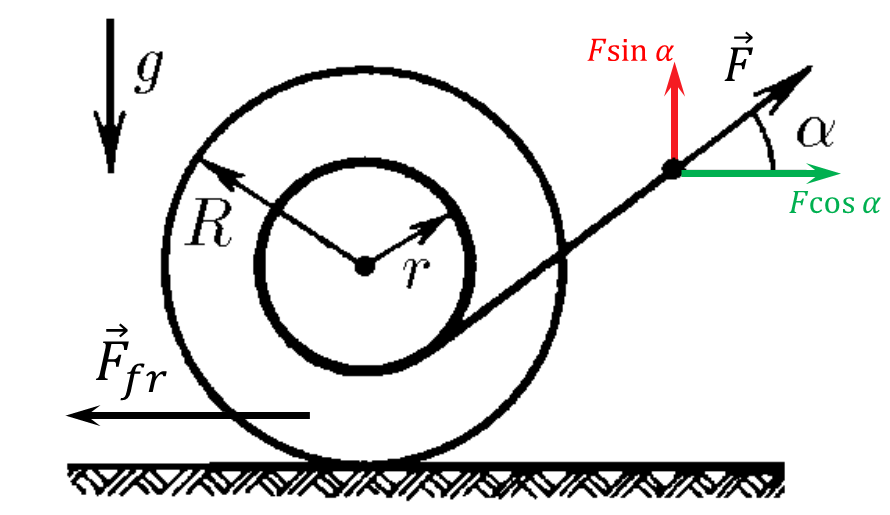
The second Newton's law for the horizontal axis $$ma=F\cos\alpha -F_{fr}\quad(1)$$ Let's write a moment of inertia with respect to the axis of rotation of the spool with angular acceleration $\varepsilon $ $$F_{fr}\cdot R - F\cdot r = \frac{mR^2}{2}\cdot \varepsilon \quad(2)$$ The moment of inertia of the spool in our model (a solid cylinder, symmetry axis) $$I=\frac{mR^2}{2}$$ Because there's no slippage: $$a=\varepsilon \cdot R\quad(3)$$ Let's substitute $(3)$ into $(1)$ $$F_{fr}=F\cos\alpha -m\varepsilon R\quad(4)$$ and put into $(2)$ $$\left(F\cos\alpha -m\varepsilon R\right)\cdot R - F\cdot r = \frac{mR^2}{2}\cdot \varepsilon $$ After algebraic transformations $$F\left(R\cos\alpha -r\right)=\frac{3mR^2\varepsilon }{2} \Leftrightarrow \boxed{\varepsilon =\frac{2F\left(R\cos\alpha -r\right)}{3mR^2}} \quad(5)$$ For the angular acceleration to be clockwise, and consequently the motion to be co-directional with the direction of $\vec{F}$, the external force moment from equation $(2)$ must be positive, and consequently the expression $(5)$ must be greater than 0. The moment of external forces in equation $(2)$ must be positive $(\varepsilon = 0)$ $$\frac{2F\left(R\cos\alpha -r\right)}{3mR^2}>0$$ $$R\cos\alpha -r>0\Leftrightarrow \boxed{\cos\alpha >\frac{r}{R}}$$ The larger the angle $\alpha$, the smaller the value of the trigonometric function $\cos\alpha$, making the expression for the angle $$\boxed{\alpha <\arccos \left(\frac{r}{R}\right)}$$
$$\cos\alpha >\frac{r}{R}$$