$2.7.27^*.$ A light rod with weights of mass $m_1$ and $m_2$ fixed to its ends rests with its middle on a rigid support. At the initial moment, the rod is held horizontally and then released. With what force does it press on the support immediately after it is released?
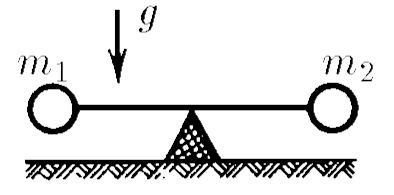

Newton's second law for a rotational movement $$M = I\varepsilon$$ $$m_1gR - m_2 g R = I\varepsilon\quad(1)$$ Since there is no slippage: $$\varepsilon = \frac{a}{R}$$ Substituting into $(1)$ $$\boxed{(m_1 - m_2) g R^2 = Ia}\quad(2)$$ Conservation of angular momentum $$I\omega = m_1vR + m_2vR\quad(3)$$ Let's express velocity through angular velocity $$v=\omega R\quad(4)$$ After substituting $(4)$ into $(3)$ $$\boxed{I = (m_1+m_2)R^2} \quad (5)$$ Let's equate the expressions $(2)$ and $(5)$ $$(m_1 - m_2) g R^2 = (m_1+m_2)aR^2$$ After mathematical transformations $$a = g \frac{m_1 - m_2}{m_1 + m_2}\quad(6)$$ Describe the forces acting on the vertical axis $$N = (m_1+m_2)g - a (m_1-m_2)\quad(7)$$ Substituting the acceleration $(6)$ into expression $(7)$ $$N = g\cdot\left((m_1+m_2)+ \frac{(m_1-m_2)^2}{m_1+m_2}\right)$$ From here we find the support reaction force: $$\boxed{N = \frac{4m_1m_2g}{m_1+m_2}}$$
$$N = 4m_1m_2g/(m_1 + m_2)$$
Mustafa Bakhodirov