$2.7.44.$ The moment of inertia of a solid body of mass $m$ relative to the $O$-axis is equal to $J$. The center of mass of the body is located at a distance $R$ from this axis. Find the force acting on the axis when a force $F$ is briefly applied to a solid body perpendicular to the segment of length $x$ that connects the point of application of the force and the axis. At which $x$ is the smallest force acting on the axis?
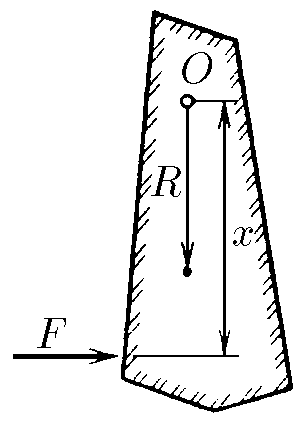
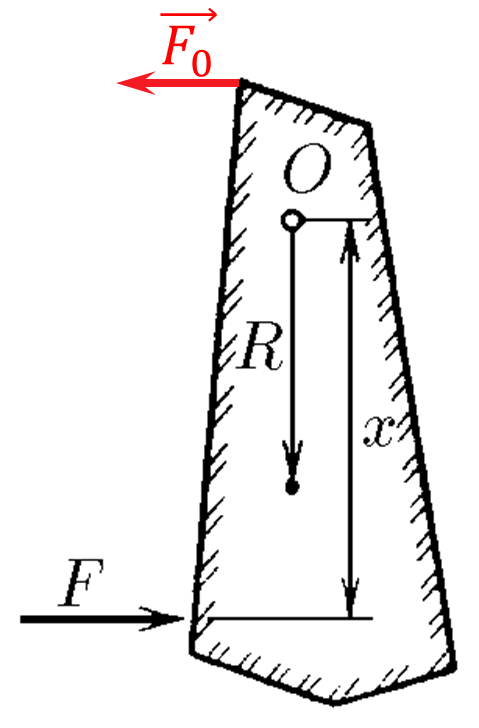
Force $\vec{F}$ creates an angular momentum $\vec{F}\cdot x$ (with $x$ perpendicular to $\vec{F}$): $$\tau_0=F\cdot x$$ $$\tau_f=J\cdot\varepsilon $$ In steady-state mode, the angular moments will be equal $$\tau_0=\tau_f=Fx=J\varepsilon $$ From where $$\varepsilon = \frac{Fx}{J}$$ Newton's second law $$F-F_0=m\varepsilon R$$ $$F_0=F-mR\cdot \frac{Fx}{J}\Leftrightarrow \boxed{F_0=F\left(1-\frac{mRx}{J}\right)}$$ From here, the minimum values of $F_0 = 0$, described by the expression $$F_0=0\Leftrightarrow 1-\frac{mRx}{J}=0$$ which will be observed at length that connects the point of application of the force and the axis $$\boxed{x=\frac{J}{mR}}$$
$F'=F(1-mRx/J)$. With $x=J/(mR),~F'=0$