$2.8.13.$ Rolling mill rolls have radius $R$. Rotating, they retract the workpiece, if its thickness is small enough. The coefficient of friction between the rolls and the workpiece is $\mu$, and the gap between the rolls is $d_0$. Find the maximum thickness of the blank. The blank is not pushed.
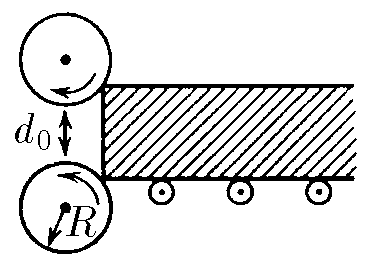
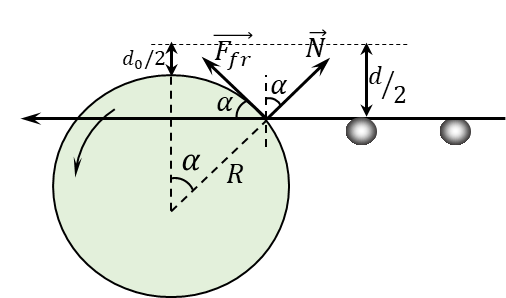
As the thickness of the workpiece increases, there will come a point where the mill rolls can no longer roll the workpiece.
It will happen until the vertical projection of friction force $\vec{F}_\text{fr}$ will exceed the vertical component of the support reaction force $\vec{N}$ $$F_\text{fr}\cos\alpha\geq N\sin\alpha$$ Considering the value of friction force $F_\text{fr} = \mu N$: $$\mu = \tan\alpha\quad(1)$$ From the drawing $$\frac{d-d_0}{2} = R(1-\cos\alpha ) \Rightarrow \boxed{d = d_0 + 2R(1-\cos\alpha )}\quad(2)$$ From the expression $(1)$, $$\cos\alpha = \frac{1}{\sqrt{1+\tan^2\alpha}}=\frac{1}{\sqrt{1+\mu^2}}\quad(3)$$ After substituting $(3)$ into $(2)$, we could obtain the maximum thickness of the blank $$\boxed{d = d_0 + 2R\left(1-\frac{1}{\sqrt{1+\mu^2}}\right)}$$
$$d_\text{max}=d_0+2R\left(1-1/\sqrt{1+\mu^2} \right)$$