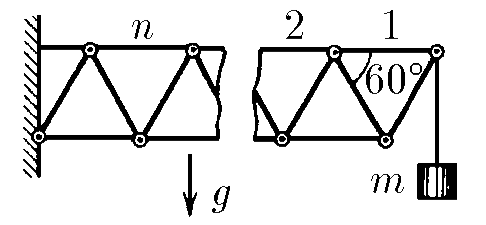
$2.8.25^*.$ A load of mass $m$ is suspended from a system of identical rods connected by hinges, as shown in the figure. Determine the force that stretches the nth upper horizontal rod.
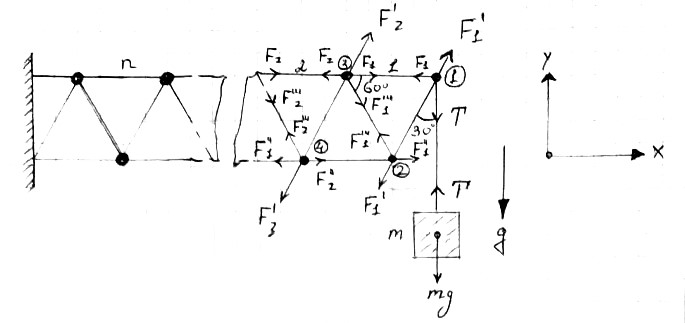
Let's consider forces acting on the 1st rod $$\left\{\begin{matrix} F_1=F_1'\cos(60^{\circ})=F_1'/2 \\ T=F_1'\cos(30^{\circ})=\sqrt{3}F_1'/2 \end{matrix}\right.$$ $$\left\{\begin{matrix} F_1'''\cos(30^{\circ})=F_1'\cos(30^{\circ}) \\ F_1'=F_1'''\\ F_1'''\cos(60^{\circ})+F_1'\cos(60^{\circ})=F_1'' \\ F_1'=F_1''\\ \end{matrix}\right.$$ And for the second rods $$\left\{\begin{matrix} F_2''\cos(30^{\circ})=F_1'''\cos(30^{\circ}) \\ F_2'=F_1'''=F_1'\\ F_2=F_2'\cos(60^{\circ})+F_1+F_1'''\cos(60^{\circ})\\ F_2=3F_1'/2 \end{matrix}\right.$$ $$F_1'=\frac{2T}{\sqrt{3}}=\frac{2mg}{\sqrt{3}}$$ $$\boxed{F_1=\frac{mg}{\sqrt{3}} \to F_2=\frac{3mg}{\sqrt{3}}}$$ As we can see, the index of $F_2$ increased by two, leading to recurrence relation for $n^\text{th}$ index: $2n-1$ $$\boxed{F_n=\frac{(2n-1)mg}{\sqrt{3}}}$$
$$T_n=(2n-1)mg/\sqrt{3}$$