$3.1.1.$ A ball is fixed in the middle of a string of length $2$l. What is the total force acting on the ball from the side of the string if its transverse displacement from the equilibrium position is $x \ll $, and the string tension force $F$ does not depend on the displacement? Why, for small displacements, can we consider the dependence of the force acting on the ball on $x$ to be linear? What is the direction of this force with respect to the displacement? Find how the potential energy of the ball depends on the small displacement $x$. What is the velocity of the ball when it passes its equilibrium position if its maximum displacement is $x_0$? The mass of the ball is $m$.
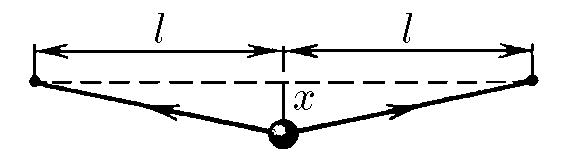
In addition to the force of gravity $mg$, the ball is subject to the force of tension of the string $F$, which has a vertical component $F'$: $$ F'=-2F\cos\alpha =-2F\frac{x}{\sqrt{l^2+x^2}}\quad(1) $$ Since the oscillations are small, we take into account that $x\ll l$ $$ \frac{x}{\sqrt{l^2+x^2}} = \frac{1}{\sqrt{1+\frac{l^2}{x^2}}} $$ Т.к. $x\ll l$, то $\frac{l^2}{x^2} \gg 1$: $$ \frac{1}{\sqrt{1+\frac{l^2}{x^2}}}=\frac{1}{\sqrt{\frac{l^2}{x^2}}}=\frac{x}{l} $$ Substituting into $(1)$ $$ \boxed{F'=-2F\frac{x}{l}} $$ We find the small change in energy as $$ dU=2F\cos\alpha dx=2F\sqrt{\frac{x}{l^2+x^2}}=2F\frac{x}{l}dx $$ Next, we integrate $dU$ from $0$ to $U$ $$ U=\int_{0}^{U}dU=\int_{0}^{x}2F\frac{x}{l}dx=\boxed{\frac{Fx^2}{l}} $$ From the law of conservation of energy, we obtain the desired speed at maximum displacement $$ \frac{Fx_0^2}{l}=\frac{m\upsilon^2}{2}\Rightarrow \boxed{\upsilon =x_0\sqrt{\frac{2F}{ml}}} $$
$$\upsilon =x_0\sqrt{\frac{2F}{ml}}$$