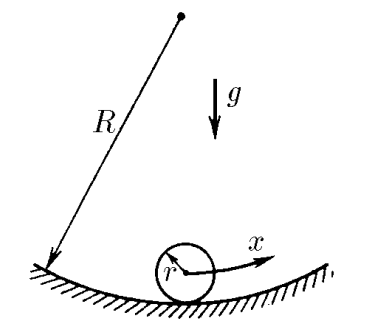
$3.1.9.$ A ball of mass $m$ and radius $r$ slides on the surface of a well whose radius of curvature is $R$. Find the dependence of the potential energy of the ball on a small displacement $x$ from the equilibrium position.
As in 3.1.5, we will propose two possible solutions: through small transformations and through integration
When the body deviates horizontally by a small value $x$, its height changes by the value $$ h=R'-\sqrt{{R'}^2-x^2}=R'\left(1-\sqrt{1-\frac{x^2}{{R'}^2}}\right)\quad(1) $$ Where $R'$ is the distance from the center of curvature to the center of mass of the ball. $$ R'=R-r $$ Considering the smallness of $x$ $$ x\ll R'\Leftrightarrow \frac{x}{R'}\ll 1 $$ So we can use approximation $(1+\xi )^a\approx 1+\xi a$, where $\xi\ll 1$ $$ \left(1-\frac{x^2}{{R'}^2}\right)^{1/2}=1-\frac{x^2}{2{R'}^2} $$ Substitute into $(1)$ $$ h=R'\cdot \frac{x^2}{2{R'}^2}=\frac{x^2}{2R'} $$ Substitute into the formula for potential energy $$ U=mgh=mg\frac{x^2}{2R'} $$ Substituting the value for $R'$, we obtain the final expression $$ \boxed{U=\frac{mgx^2}{2(R-r)}} $$
The change in energy with a small change in coordinate can be found by definition $$ dU=Fdx $$ In this case, we will find the horizontal force that will return the ball to stable equilibrium taking into account the smallness of the angle $\varphi$ $$ F=mg\sin\varphi=mg\frac{x}{R-r} $$ Where we find the potential energy through integration $dU$ $$ U=\int_{0}^{U}dU=\int_{0}^{x}mg\frac{x}{R-r}dx=\frac{mg}{R-r}\int_{0}^{x}xdx $$ This integral is solved as $$ \int_{0}^{x}xdx=\frac{mg}{R-r}\cdot\frac{x^2}{2} $$ Where does the potential energy of the ball come from? $$ \boxed{U=\frac{mgx^2}{2(R-r)}} $$
$$U=\frac{mgx^2}{2(R-r)}$$