Statement

$3.2.11.$ Find the frequency of small oscillations of the system described in problem 3.1.10

Solution

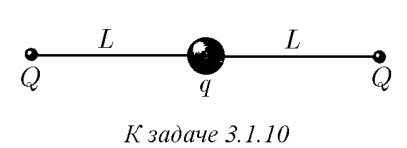
Newton's Second Law $$ m\ddot{x}(t)-F=0 $$ Where we find the total external force from Coulomb's law $$ F=kqQ\left(\frac{1}{(L-x)^2}-\frac{1}{(L+x)^2}\right) $$ Using the approximation for a small value $$ x =\frac{h}{R} \ll 1; \quad(1+x)^\alpha\approx 1+\alpha x $$ $$ F=-\frac{4kqQLx}{(L^2-x^2)^2}\approx-\frac{4kqQx}{L^3} $$ Harmonic oscillation equation $$ \ddot{x}(t)+\frac{4kqQx}{mL^3}x(t) $$ We obtain the required frequency of small oscillations $$ \boxed{\omega =\sqrt{\frac{4kqQ}{mL^3}}=\sqrt{\frac{qQ}{m\pi\varepsilon_0L^3}}} $$

Answer

$$\omega =\sqrt{\frac{qQ}{m\pi\varepsilon_0L^3}}$$