$3.2.13.$ A straight tunnel is dug in the Earth that does not pass through its center. Determine the time of movement of a train with engines turned off through such a tunnel if the influence of the Earth's rotation on the movement of the train and friction are neglected.
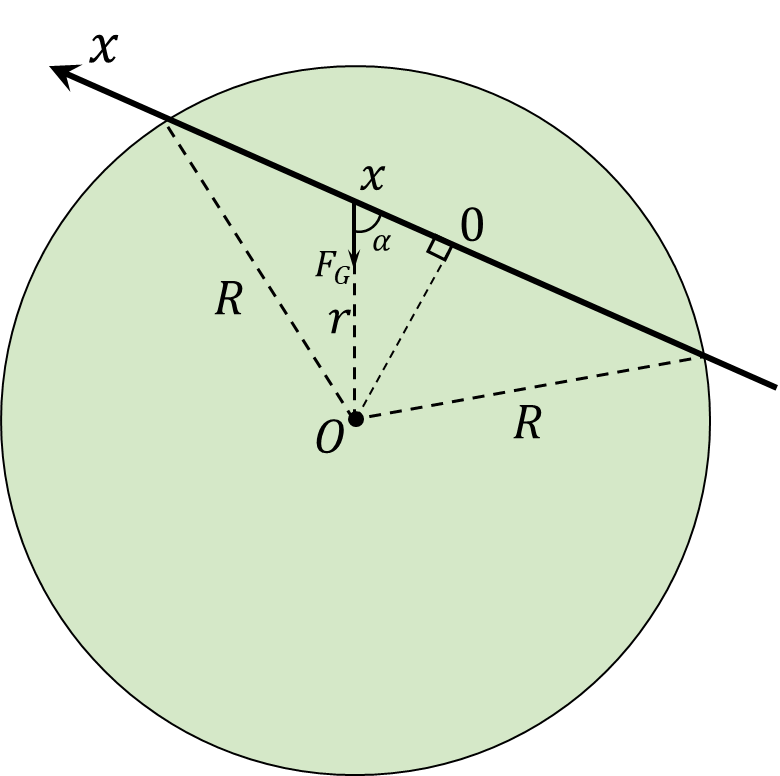
Similarly to 3.2.12, we find the external force $F$ as
The body, at a distance $x$ from the core, will be affected by the gravitational force of attraction caused by the inner layers of the planet with density $\rho$, forming a sphere of radius $x$. The mass of this part of the earth $$ M_\oplus = \frac{4}{3} \rho\pi x^3 $$ Gravitational force acting on a rock at depth $x$ $$ F_G = \frac{GmM_\oplus}{x^2}=mg\frac{x}{R} $$ In this case, only the horizontal component of this force will create a moment. Whence, the resulting external force is equal to $$ F=mg\cos\alpha =mg\frac{x}{R} $$ From here we find the angular frequency of oscillations $$ \omega =\sqrt{\frac{g}{R}} $$ The period of oscillation in a given system $$ T=2\pi\sqrt{\frac{R}{g}} $$ Since we are interested in the flight time only in one direction, we take half of this period. $$ \boxed{t=\frac{T}{2}=\pi\sqrt{\frac{R}{g}}\approx42\text{ min}} $$
$$t=42\text{ min}$$