$3.2.14.$ A board of mass $m$ lies on two rollers rotating with high speed towards each other. The distance between the axes of the rollers is $L$, the coefficient of friction when the board slides on the roller is $\mu$. Find the frequency of longitudinal oscillations of the board.
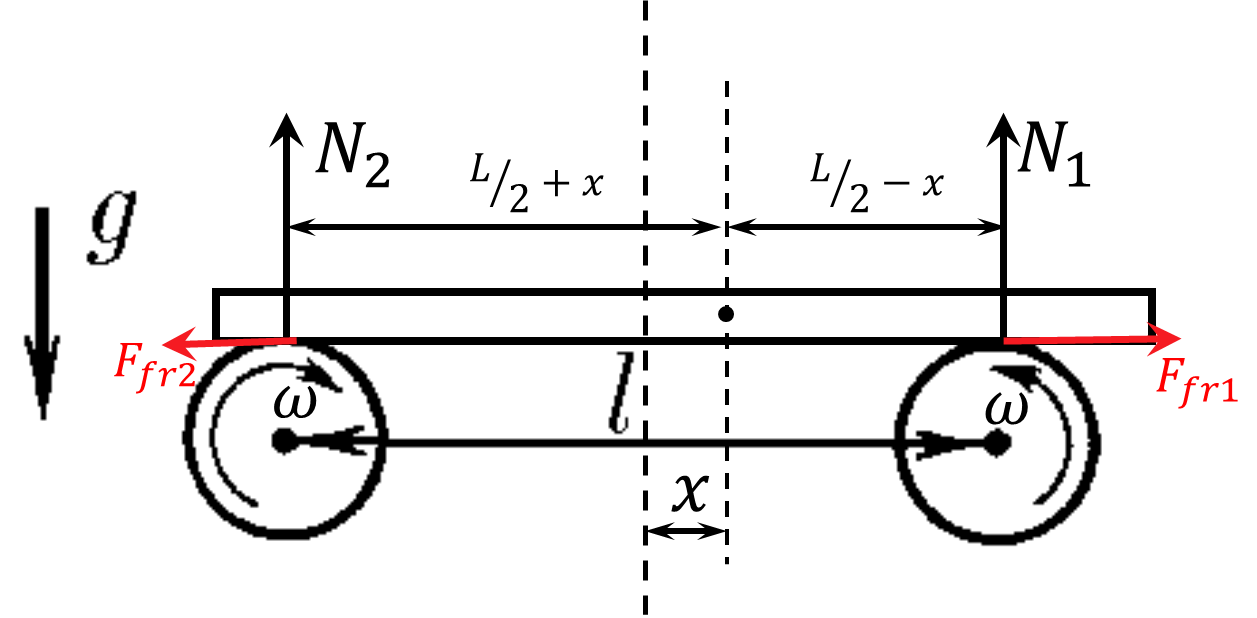
Newton's second law for the horizontal axis $$ ma=F_{fr1}-F_{fr2} $$ Equilibrium condition for the vertical axis $$ mg=N_1+N_2\quad(1) $$ In the equilibrium condition, the sum of the moment of external forces must be equal to zero. $$ N_1\left(\frac{l}{2}-x\right)-N_2\left(\frac{l}{2}+x\right)=0 $$ Where does the reaction force on the second support come from? $$ N_2=N_1\left(\frac{L/2-x}{L/2+x}\right) $$ Substitute into $(1)$ $$ mg=N_1\left(1+\frac{L/2-x}{L/2+x}\right) $$ $$ N_1=mg\left(\frac{L/2+x}{L}\right);\quad N_2=mg\left(\frac{L/2-x}{L}\right) $$ Newton's second law for the horizontal axis $$ m\ddot{x}=\mu N_2-\mu N_1= - \mu mg \frac{2x}{L}\quad(2) $$ We transform the obtained expression and obtain the equation of harmonic oscillations $$ \ddot{x}(t)+\frac{2\mu g}{l}x(t)=0 $$ Where does the angular frequency of oscillations come from? $$ \boxed{\omega =\sqrt{\frac{2\mu g}{l}}} $$
$$\omega =\sqrt{\frac{2\mu g}{l}}$$