$3.2.16.$ A heavy cart rolls with acceleration $a$ on an inclined plane forming an angle $\alpha$ with the horizon. Find the period of oscillation of a pendulum of length $l$ mounted on the cart.
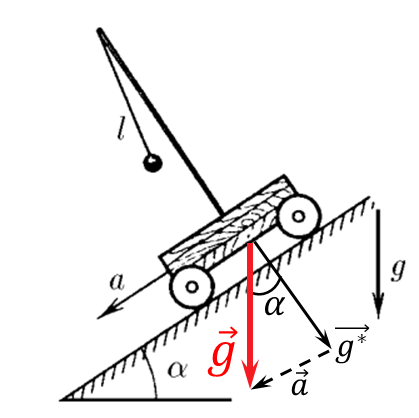
The period of oscillation of a pendulum on an inclined cart can be found using the well-known formula for the period of oscillation of a mathematical pendulum, by switching to the inertial frame of reference of the cart $$ T=2\pi\sqrt{\frac{l}{g^*}}\quad(1) $$ Where $\vec{g}^*$ is the acceleration of the inertial reference frame $$ \vec{g}^*=\vec{g}-\vec{a} $$ Using the cosine law, we find the value of the modulus of the vector $\vec{g}^*$ $$ (g^{*})^2=a^2+g^2-2ag\cos\alpha$$ Where $$ \boxed{g^*=\sqrt{a^2+g^2-2ag\cos\alpha}} $$ We substitute $(1)$ into the expression and find the period of oscillation of the pendulum $$ \boxed{T=2\pi\sqrt{\frac{l}{\sqrt{a^2+g^2-2ag\cos\alpha}}}} $$
$$T=2\pi\sqrt{l/{\sqrt{a^2+g^2-2ag\cos\alpha}}}$$