$7.1.12^*.$ Determine what the accelerating potential difference $V$ should be in order for the electrons to follow the path shown in the figure. Radii of cylindrical capacitor plates $R_1$ and $R_2$. Potential difference between the plates $V_0$.
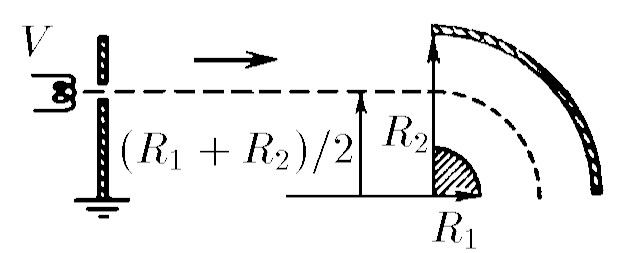
Gauss theorem $$\oint_{2\pi r}E\,dl=\frac{q}{\varepsilon_0}\Rightarrow E=\frac{q}{2\pi\varepsilon_0 r}$$ Let's write down the small change of the electrostatic field and then integrate it $$dU=E \,dr\Rightarrow \int dU=\int E \,dr$$ Integrate from $R_1$ to $R_2$ $$U_0=\frac{q}{2\pi\varepsilon_0 r}\int_{R_1}^{R_2}\frac{dr}{r}=\frac{q}{2\pi\varepsilon_0 r}\ln\frac{R_2}{R_1}$$ Law of conservation of energy $$\frac{mv^2}{2}=eU$$ $$e\frac{q}{2\pi\varepsilon_0 \frac{R_1+R_2}{2}}=\frac{mv^2}{(\frac{R_1+R_2}{2})}$$ From where we get $$\frac{q}{2\pi\varepsilon_0}=\frac{mv^2}{e}$$ Substituting the previously obtained values $$\frac{U_0}{\ln\frac{R_2}{R_1}}=\frac{2eU}{e}$$ From where $$U=\frac{U_0}{2\ln\frac{R_2}{R_1}}$$
$$V=(V_0/2)/\ln(R_2/R_1)$$