$7.1.23^*.$ Find the period of small vibrations of a body of mass $m$, whose charge is $q$, inside a smooth sphere of radius $R$, if the charge $Q$ is fixed at the top point of the sphere.
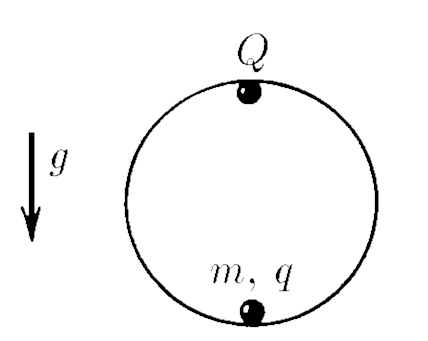

Considering the fact that oscillations are small, $\varphi \ll 1$, we could use the approximations for small angle $\varphi$ $$\sin\varphi \approx \varphi; \quad\cos\varphi \approx 1\quad(1)$$ From where, we could approximate that the distance between charges remains approximately the same $$r\approx2R$$ Thus, the сoulomb's law for two charges $$F_c = \frac{1}{4\pi\varepsilon_0}\frac{qQ}{4R^2}$$ Let's write Newton's second law on a tangential trajectory, in the direction of motion of a charge of mass $m$ $$ma = mg \sin\varphi + F_c \sin\frac{\varphi}{2}$$ Considering the approximation $(1)$ and the expression $$ma = -mg\frac{x}{R} - \frac{x}{2R} \frac{1}{4\pi\varepsilon_0}\frac{qQ}{4R^2}$$ $$a = -x\left(\frac{g}{R}+\frac{qQ}{32\pi\varepsilon_0mR^3}\right)$$ Solving the equation of harmonic oscillations $(\ddot{x}+\omega^2x(t)=0)$, we could obtain the value for angular velocity $$\omega =\sqrt{\frac{g}{R}+\frac{qQ}{32\pi\varepsilon_0mR^3}}$$ From here the period of oscillation $$\boxed{T=\frac{2\pi}{\omega} = \frac{2\pi}{\sqrt{\frac{g}{R}+\frac{qQ}{32\pi\varepsilon_0mR^3}}}}$$ Since the expression under the square root cannot be less than zero, the ratio at which there will be no oscillations $$\frac{g}{R}+\frac{qQ}{32\pi\varepsilon_0mR^3} > 0 \Leftrightarrow \boxed{\frac{qQ}{32\pi\varepsilon_0R^2}>-mg}$$
$$T=2\pi\left(\frac{g}{R}+\frac{qQ}{32\pi\varepsilon_0mR^3}\right)^{-1/2}\text{ with }\frac{qQ}{32\pi\varepsilon_0R^2}>-mg$$