$7.3.9^*.$ A thin electron beam accelerated by the potential difference $V$ enters a flat capacitor parallel to its plates. Determine the angular spread of electrons if a voltage $V_0$ sin wt is applied to the capacitor plates. The distance between the plates of the capacitor $d$ is much smaller than its length $l$.
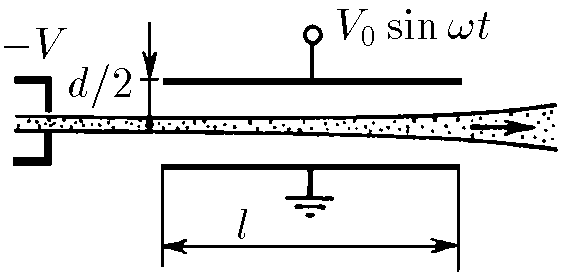
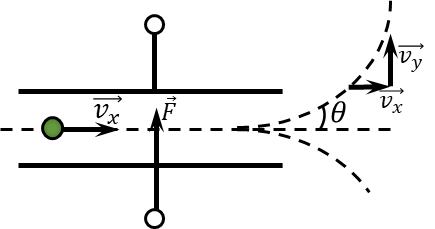
From the drawing $$\tan\alpha = \frac{v_y}{v_x}$$ Law of conservation of energy $$\frac{mv^2_x}{2}=eU$$ From where $$v_x=\sqrt{\frac{2eU}{m}}$$ Force $\vec{F}$ acting on the particle: $$F=eU=e\frac{U_0}{d}\sin\omega t$$ Second Newton's Laws $$ma=\frac{eU_0}{d}\sin\omega t$$ By the definition of acceleration $a = \frac{dv}{dt}$ $$\frac{dv}{dt}=\frac{eU_0}{md}\sin\omega t$$ Let's regroup and integrate $$\int _0^{v_y}dv=\frac{eU_0}{md}\int_0^t\sin\omega t\,dt$$ $$v_y=\frac{eU_0}{md\omega}(1-\cos\omega t)$$ Time for which the particle will move horizontally by the value $l$ $$t=\frac{l}{v_x}=l\sqrt{\frac{m}{2eU}}$$ Find the angle of velocity to the horizontal $$\tan\theta = \frac{v_y}{v_x}=\frac{eU_0}{m\omega d}\sqrt{\frac{m}{2eU}} \left( 1-\cos\omega l \sqrt{\frac{m}{2eU}}\right)$$ Whence the angle $\angle \theta$ $$\boxed{\theta =\operatorname{\arctan } \left( \frac{U_0}{\omega d}\sqrt{\frac{e}{2mU}} \bigg[ 1-\cos\omega l \sqrt{\frac{m}{2eU}}\bigg] \right)}$$ A little extra. Given that $d \ll l$ we can use the approximation $\tan x \approx x$ $${\theta = \frac{U_0}{\omega d}\sqrt{\frac{e}{2mU}} \bigg[ 1-\cos\omega l \sqrt{\frac{m}{2eU}}\bigg] }$$ Find the required scattering angle $${\Delta \alpha =2\theta = \frac{U_0}{\omega d}\sqrt{\frac{2e}{mU}} \bigg[ 1-\cos\omega l \sqrt{\frac{m}{2eU}}\bigg] }$$
$$\Delta\alpha =\pm\operatorname{\arctan }\bigg\{\frac{V_{0}}{d\omega}\sqrt{\frac{2e}{m_{e}V}}\bigg[1-\operatorname{cos}\bigg(\omega l\sqrt{\frac{m_{e}}{2eV}}\bigg)\bigg]\bigg\}$$