$9.1.10.$ Prove that the moment of force acting on any flat frame with current in a uniform magnetic field of induction $B$ is $\vec{N} = [\vec{M} \times \vec{B}]$.
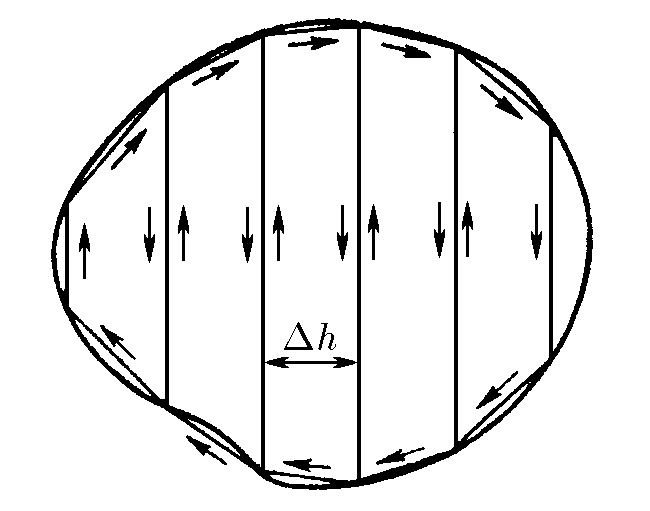
Let's break up an arbitrary contour with vertical lines, these lines will not make any changes at the moment since on one side the current goes in one direction, and in the adjacent contour in the opposite direction, then for a sufficiently small breakdown these will be frames for which we have already proved this statement, then the general $$ \vec{N} =\int{d\vec{N}} = \int{[d\vec{M} \times \vec{B}]} $$ in scalar form will look like: $$ {N} =\int{d{M}{B}\sin\alpha}= BM\cdot \sin\alpha $$ since the direction of $\vec N$ and $\vec M$ coincides for all small frames, it is true that $\vec N$ and $d\vec N$ are co-directed, then it is obvious that: $$ \boxed{\vec{N} = [\vec{M} \times \vec{B}]} $$