$9.1.11.$ a) A wire frame in the form of a circle with current can rotate about the horizontal axis $OO^\prime$. The mass of a unit length of the wire is $\rho$, the current in the frame is $I$. The frame is in a magnetic field of induction B, directed along the gravitational field. Determine the angle of deviation of the plane of the circle from the vertical.
b) A wire frame in the form of a circle has a wire jumper along the diameter, parallel to the horizontal axis $OO^\prime$, about which the frame can rotate. The mass of a unit length of the frame and the jumper is the same and is equal to $\rho$. The current entering the frame is equal to $I$. The frame is in a magnetic field of induction $B$, directed parallel to the gravitational field. At what angle from the vertical will the frame deviate?
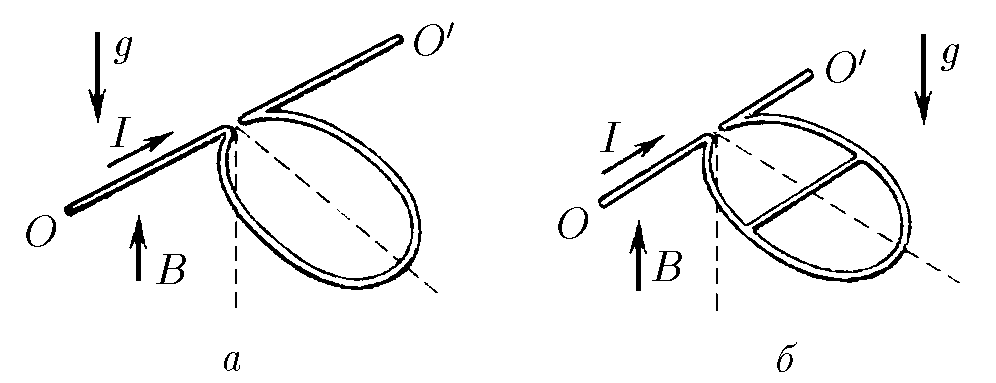
a) Using the expression for the moment of magnetic field obtained in 9.1.10, $\vec{N} = [\vec{M} \times \vec{B}]$ we obtain $$ N = BIS\cdot \cos\alpha = \pi R^2BI \cdot \cos\alpha $$ in this case the moment of gravity: $$ M_{mg} = Rmg\cdot \cos\alpha = 2\pi R^2\rho g\cdot \sin\alpha $$ these moments are equal: $$ 2\pi R^2\rho g \cdot \sin\alpha = \pi BI R^2 \cdot \cos\alpha $$ after transformations, we obtain $$ \boxed{\tan\alpha = \frac{BI}{2\rho g}} $$ b) Find the moment of gravity: $$ M_{mg} = mgR\cdot \sin\alpha = (2\pi R + 2R)\rho gR \cdot \sin\alpha $$ $$ M_{mg} = 2R^2\rho g(1+\pi ) \cdot \sin\alpha $$ Now, we represent the initial circuit as two superimposed circuits with currents $I_1$ and $I_2$ such that $I = I_1 + I_2$, the circuit with $I_2$ is a semicircle with a partition, the circuit with $I_1$ is a ring without a partition, then from the parallel connection it follows that: $I_1\cdot \pi R = I_2 \cdot 2R$ then $$ I_1 = I_2\cdot \frac{2}{\pi} $$ $$ I = I_1 + I_2 = I_2\left(1+\frac{2}{\pi}\right) $$ $$ I_1 = I\cdot \frac{2}{\pi +2}; \quad $$ Then the moments for these contours are: $$ M_{k1} = BS_1\cdot \cos\alpha =\pi R^2I\cdot \frac{2}{\pi +2}B\cdot \cos\alpha $$ $$ M_{k2} = BS_2\cdot \cos\alpha = \frac{1}{2}\pi R^2I\cdot \frac{\pi}{\pi +2}B\cdot \cos\alpha $$ Total moment of the contours: $$ M_k = \frac{1}{2}\pi R^2 BI \cdot \cos\alpha\cdot \frac{\pi + 4}{\pi +2} $$ Let's equate this moment and the moment of gravity: $$ \frac{1}{2}\pi R^2 BI \cdot \cos\alpha\cdot \frac{\pi + 4}{\pi +2} = 2R^2\rho g(1+\pi ) \cdot \sin\alpha $$ from here $$ \boxed{\tan\alpha = \frac{\pi (\pi +4)}{4(\pi +2)(\pi +1)} \cdot \frac{BI}{\rho g}} $$
$$\tan\alpha = \frac{\pi (\pi +4)}{4(\pi +2)(\pi +1)} \cdot \frac{BI}{\rho g}$$