$9.1.12.$ A coil of radius $R$ was bent along its diameter at a right angle and placed in a uniform magnetic field of induction B so that one of the planes of the coil was located at an angle $\alpha$, the other at an angle $\frac{\pi}{2}-\alpha$ to the direction of induction $B$. The current in the coil is $I$. Determine the moment of forces acting on the coil.
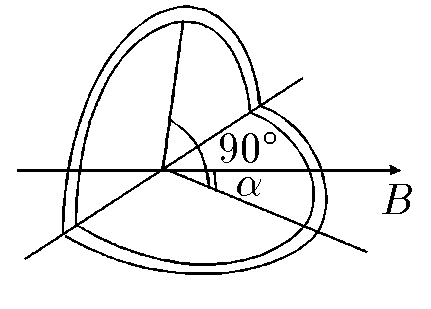
Let's split the circuit into two circuits with the same current, but in different planes.
Let's find the moment of forces for each of them: $$ M_1 = \frac{1}{2}\pi R^2IB\cdot \sin\alpha $$ $$ M_2 = \frac{1}{2}\pi R^2IB\cdot \sin\left(\frac{\pi}{2} -\alpha\right) = \frac{1}{2}\pi R^2IB\cdot \cos\alpha $$ Total moment of forces $$ \boxed{M = M_1 + M_2 = \frac{1}{2}\pi R^2IB\cdot (\sin\alpha + \cos\alpha )} $$
$$M = \frac{1}{2}\pi R^2IB\cdot (\sin\alpha + \cos\alpha )$$