$9.1.8^*.$ A square frame with current is located in a uniform magnetic field of induction $B$. The frame mass is $m$, and the current in it is $I$. Determine the frequency of free oscillations of the frame around the $OO^\prime$ axis.
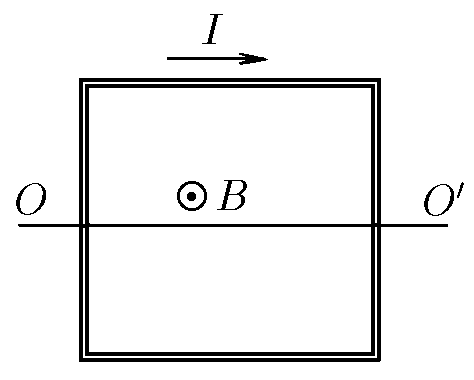
Let's consider a small deviation from equilibrium by an angle $\alpha$:
The moment acting on the frame from the magnetic field: $$ M = BIS\cdot \sin\alpha = BIa^2 \sin\alpha $$ where $a$ is the side of the frame
gravity does not create a moment as it passes through the point of rotation
From the basic equation of rotational motion: $$ J\ddot{\alpha} = \sum\pm{M_i} $$ for our case: $$ J\ddot{\alpha} = -BIa^2 \sin\alpha\quad (1) $$ now we will find the moment of inertia $J$ of the frame during the observed oscillations
The moment of inertia of the upper and lower sides of the frame is $$ J_1=J_2 = \frac{m}{4}\cdot \left(\frac{a}{2}\right)^2 = \frac{m a^2}{16}\quad (2) $$ where $a/2$ is the distance to this side.
Moment of inertia of the lateral sides: $$ J_3 = J_4 = \frac{1}{12} \cdot \frac{m}{4}\cdot a^2 = \frac{m a^2}{48}\quad (3) $$ We find the moment of inertia $J$ by substituting $(2)$ and $(3)$ $$ J = J_1 + J_2 + J_3 + J_4 $$ $$ J = 2\cdot \frac{m a^2}{16} + 2 \cdot \frac{m a^2}{48} = \frac{m a^2}{6} $$ then equation $(1)$ will look like: $$ \frac{m a^2}{6}\ddot{\alpha} = -BIa^2 \sin\alpha $$ $$ \ddot{\alpha} = -\frac{6BI}{m} \alpha (t) $$ Solving the equation of harmonic oscillations, we find the oscillation frequency $$ \boxed{\omega = \sqrt{\frac{6BI}{m}}} $$
$$\omega = \sqrt{\frac{6BI}{m}}$$