$9.1.9.$ A triangular wire frame with current can rotate about a horizontal axis $OO^\prime$ passing through the vertex of the triangle. The mass of a unit length of wire is $\rho$, the current in the frame is $I$. The frame is in a magnetic field of induction $B$ directed along the gravitational field. Determine the angle of deviation of the plane of the triangle from the vertical.
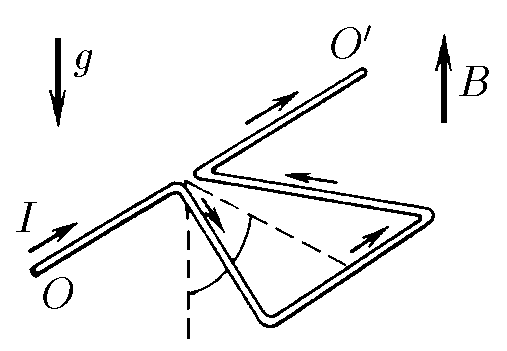
To solve this, we will use the fact that $\vec{N} = \vec{M} \times \vec{B}$ is valid for any contour $S$ with magnetic moment $M$ (for the proof, see 9.1.10)
The moment of magnetic field forces $$ N_{B} = |\vec{M} \times \vec{B}| = ISB \cos\alpha\quad(1) $$ The center of mass will be at the intersection point of the medians, the distance from this point to the suspension point: $$ h_C=\frac{2h}{3} $$ Moment of gravity $$ M_{mg} = 3a\rho g\cdot \frac{2}{3}h \sin\alpha\quad(2) $$ where $a$ is the side of the triangle, and its area $S = \frac{1}{2}ah$ We substitute the result into $(2)$ $$ M_{mg}= 4S\rho g\cdot \sin\alpha\quad(3) $$ We equate the obtained moments from $(1)$ and $(3)$: $$ ISB\cdot \cos\alpha = 4S\rho g \cdot \sin\alpha\Rightarrow \boxed{\tan\alpha = \frac{IB}{4\rho g}} $$
$$\tan\alpha = \frac{IB}{4\rho g}$$