$9.2.13.$ A long straight wire with current $I$ has a section in the form of a semicircle of radius $R$. Determine the magnetic field induction at the center of the semicircle.
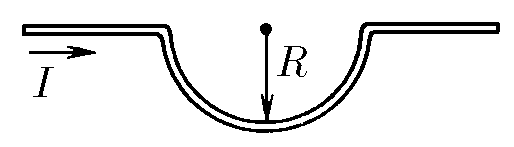
Let's write down the expression for the induction of a section of wire $$ d\vec B = \frac{\mu_0 [\vec{(Idx)}\times \vec{R}]}{4\pi R^3} $$ We find the modulus of the vector $d\vec B$ by transforming the vector product $$ dB = \frac{\mu_0 Idx}{4\pi R^2}\sin\alpha $$ Where $\alpha$ is the angle between the radius vector and the direction of the current element. Given that they coincide, then $\alpha = 0$: $$ \sin\alpha = 0\Rightarrow dB = 0 $$ For a straight section of wire, then such a design creates a field similar to the field of the semicircle, which we already calculated in 9.2.11 $$ \boxed{B = \frac{\mu_0 I}{4R}} $$
$$B=\frac{\mu_0 I}{4R}$$