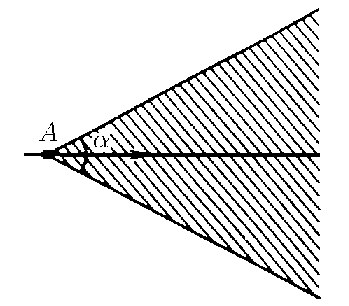
$1.1.10^{∗}$ По прямому шоссе идет автобус с постоянной скоростью $v$. Вы заметили автобус, когда тот находился в некоторой точке $A$. Из какой области около шоссе вы можете догнать этот автобус, если скорость вашего бега $u < v$? Нарисуйте эту область для $u = v/2$
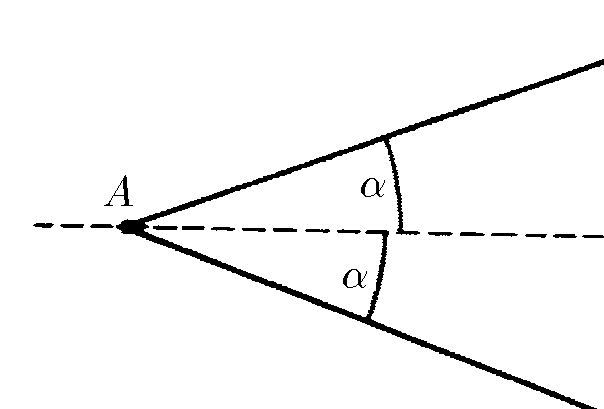

1. Пусть автобус находится в точке $А$, а догоняющий начинает движение из точки $В$ и бежит перпендикулярно дорожному полотну $АС$. Введём обозначения: $АС = L, BC = h, AB = s.$
2. Из прямоугольного треугольника $АВС$ имеем
$$L = s \cdot \cos\frac{\alpha}{2}\text{ и }h = s \cdot\sin\frac{\alpha}{2}$$
3. Время движения автобуса $t_1$ и пассажира $t_2$ до встречи в точке $С$
${t}_{1}=\frac{{L}}{{v}}=\frac{{s}\cos(\alpha /2)}{{v}};\quad{t}_{2}=\frac{{h}}{{u}}=\frac{{s}\sin(\alpha /2)}{{u}}$
откуда
$$\fbox{$\alpha = 2 \cdot \arctan \frac{u}{v}$}$$