$1.1.12^{∗}$ Два стержня пересекаются под углом $2\alpha$ и движутся с равными скоростями $v$ перпендикулярно самим себе. Какова скорость точки пересечения стержней?
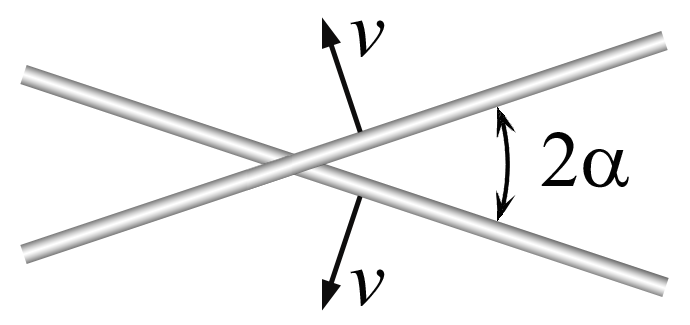
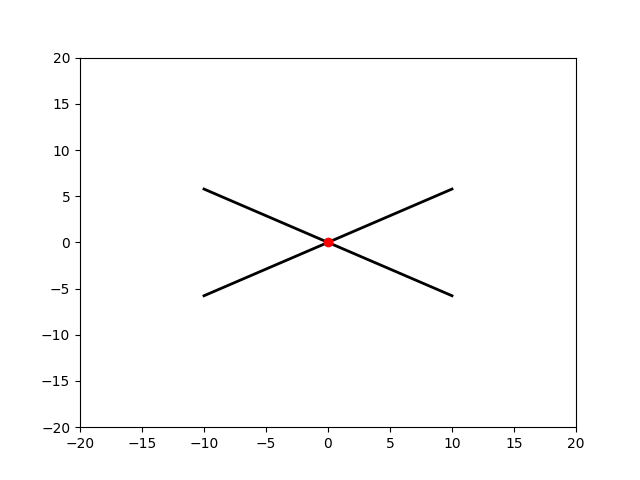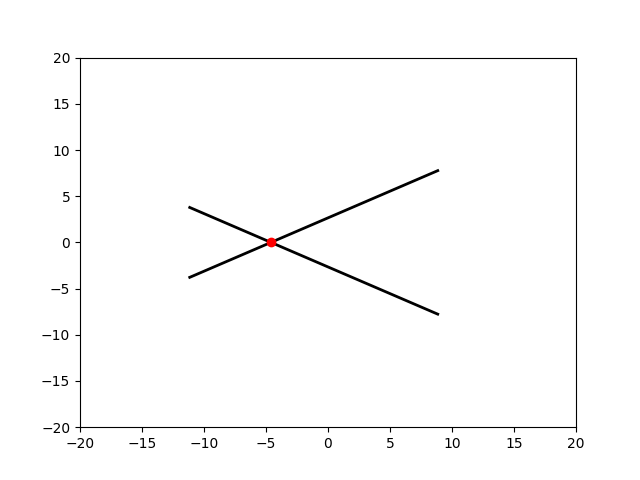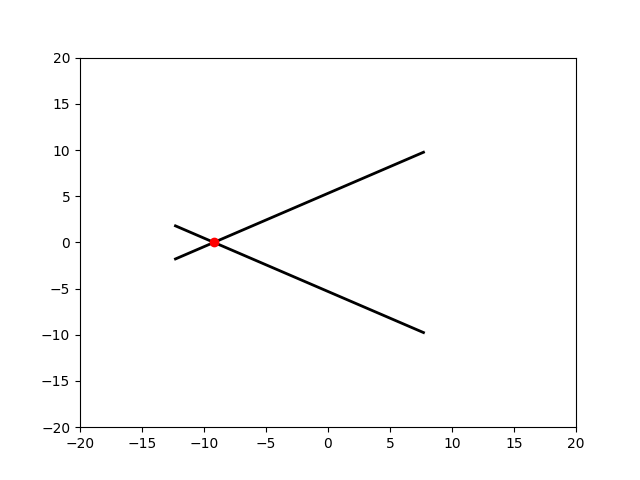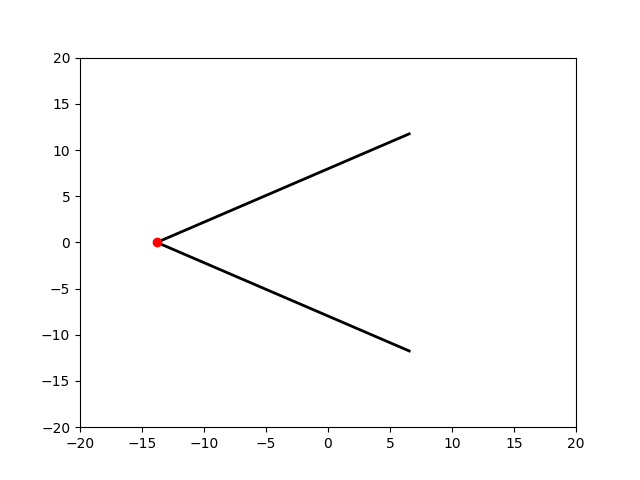
Как показано на анимации, при движении точка пересечения будет оставаться на биссектресе угла $2\alpha$ между ними
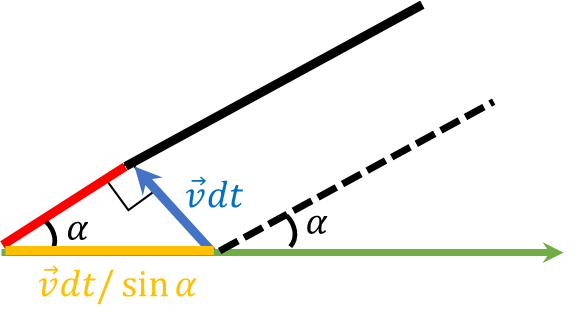
Рассмотрим изменение точки пересечения на горизонтальной оси в течении промежутка времени $dt$
Из геометрии прямоугольного треугольника, горизонтальная координата(она же гипотенуза) изменилась на $dx = v dt / \sin\alpha$
Откуда скорость:
$$\fbox{$u = \frac{dx}{dt} = \frac{v}{\sin\alpha}$}$$
$$u = v/ \sin\alpha$$