Условие:

$1.1.20^*.$ По биллиардному столу со сторонами $а$ и $б$ пускают шар от середины стороны $b$. Под каким углом к борту стола должен начать двигаться шар, чтобы вернуться в ту же точку, из которой он начал свое движение?

Решение:

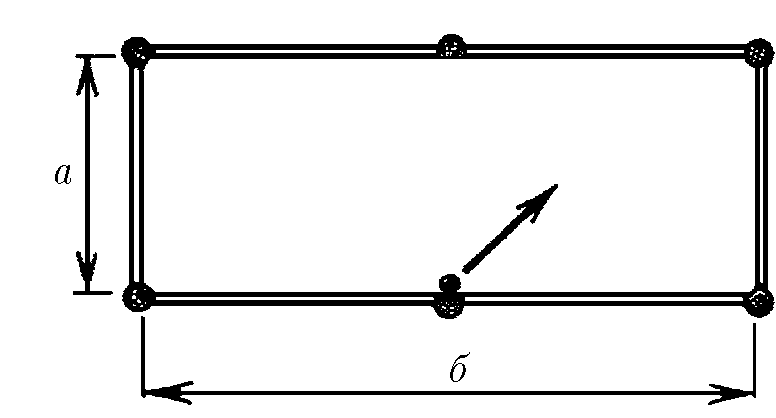
По-аналогии с 1.1.18, можно воспользоваться Методом Изображений и представить упругие стенки как оптические зеркала.

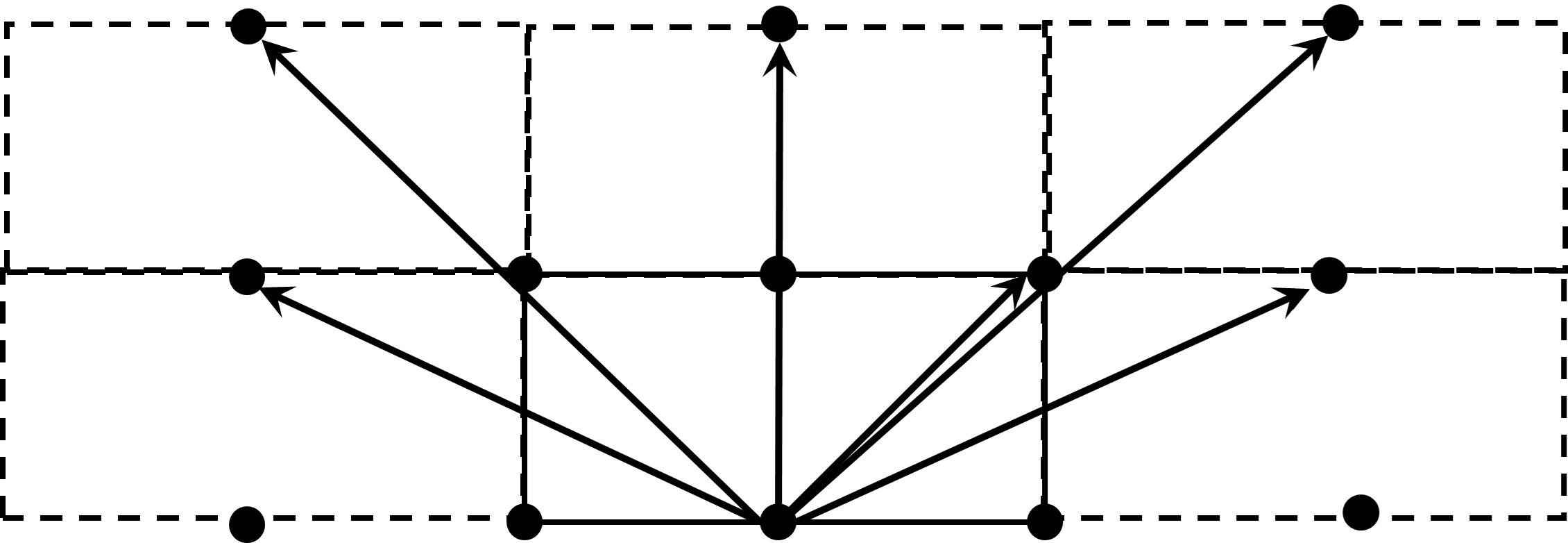
Чтобы попасть в исходное положение, нужно всего лишь попасть в любую из лунок-изображений.

Координаты лунок описываются выражением:

$x=2ma$ и $y=nb$, где $m$ и $n$ — любые целые числа

Откуда искомый угол:"

$\alpha = \arctan (2ma/(nb))$

Ответ: $\tan\alpha = 2ma/(nb)$, где $m$ и $n$ — любые целые числа