$1.1.21.$ Уголковый отражатель, установленный на луноходе, представляет собой три взаимно перпендикулярных зеркала. Если на отражатель падает свет, скорость которого $c = (c_x, c_y, c_z)$, то какие составляющие будет иметь скорость света после отражения от зеркала, находящегося в плоскости $yOz$? после отражения от всех трех зеркал?
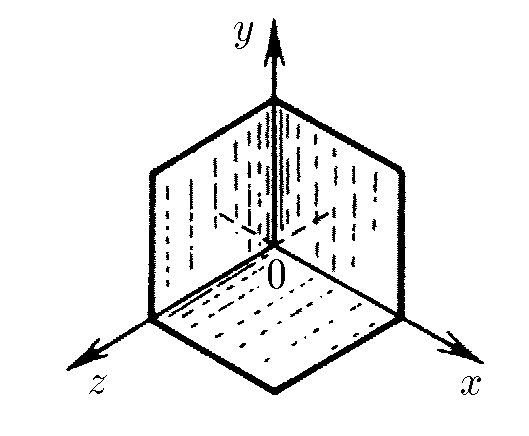
$(a)$ Так как зеркало в плоскости $yOz$ отражает луч вдоль оси $Ox$, координата $x$ инвертируется.
Таким образом, если $\vec{c_1}$ - отраженный луч от $\vec{c}$,
$\vec{c_1} = (-c_x, c_y, c_z)$
$(b)$ Аналогично, зеркала в плоскостях $yOx$ и $xOz$ отражают луч вдоль осей $Oz$ и $Oy$, соответственно:
$\vec{c_2} = (c_x, c_y, -c_z)$, для $yOx$
$\vec{c_3} = (c_x, -c_y, c_z)$, для $xOz$
При отражении от сразу трех зеркал, все компоненты $\vec{c}$ примут свои отрицательные значения:
$\vec{c_4} = (-c_x, -c_y, -c_z)$