$1.1.22.$ Внутри закрепленного гладкостенного цилиндра радиуса $R$ летает маленький шарик, упруго отражаясь от стенок так, что минимальное расстояние от него до оси цилиндра равно $h$. Какую долю времени он находится на расстоянии от оси цилиндра, меньшем $r$, но большем $h$?
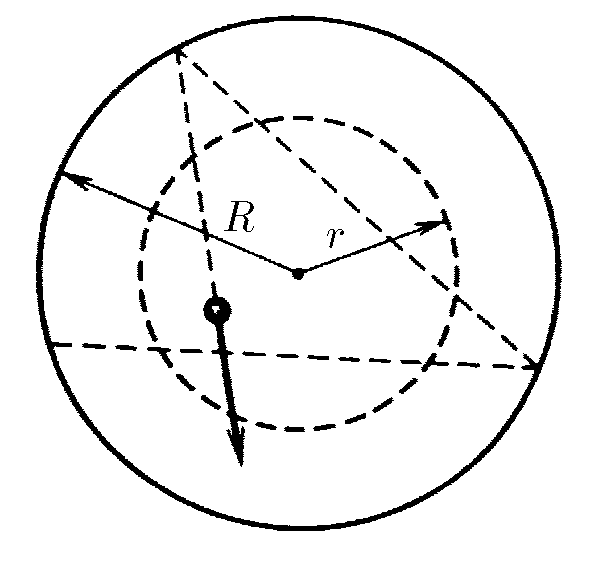
Рассмотрим движени шарика, описаного в условии задачи
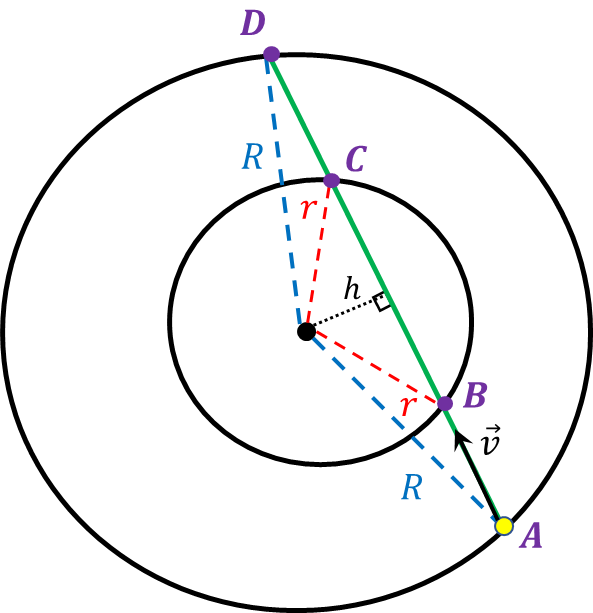
Т.к. между соударениями скорость удара не меняется, а удары абсолютно упругие, то можно считать скорость неизменной. Следовательно, за равные промежутки времени тело, проходит равные расстояния.
Тогда искомое отношение $\frac{\Delta t}{t}$, найдем как отношение $\frac{BC}{AD}$
$$\frac{\Delta t}{t} = \frac{BC}{AD}$$
По теореме Пифагора:
$BC = 2 \sqrt{r^2-h^2}$
$AD = 2 \sqrt{R^2-h^2}$
Отсюда
$$\frac{BC}{AD} = \frac{\sqrt{r^2-h^2}}{\sqrt{R^2-h^2}}$$
Или
$$\frac{\Delta t}{t} = \frac{\sqrt{r^2-h^2}}{\sqrt{R^2-h^2}}$$