$1.1.4.$ Счетчики $A$ и $B$, регистрирующие момент прихода $\gamma$-кванта, расположены на расстоянии $2 \, м$ друг от друга. В некоторой точке между ними произошел распад $\pi^{0}$ -мезона на два $\gamma$-кванта. Найдите положение этой точки, если счетчик $A$ зарегистрировал $\gamma$-квант на $10^{−9}$ с позднее, чем счетчик $B$. Скорость света $3\cdot 10^{8} \, м/с$
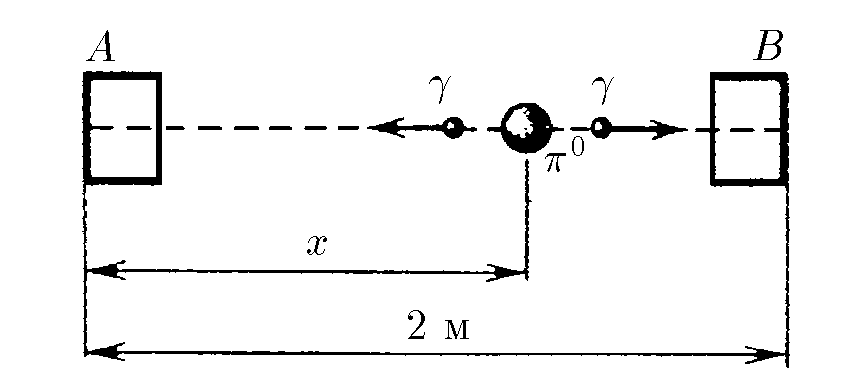
1. Введём следующие обозначения
$$x_B=L-x$$
$$t_A=t_B+\Delta t$$
2. Время полёта $\gamma$-кванта до счётчиков
$$t_B+\Delta t=\frac{x}{c}$$
$$t_B=\frac{L-x}{c}$$
3. Решая уравнения совместно, получим
$$\frac{L-x}{c} + \Delta t = \frac{x}{c}$$
$$x= \frac{L+c\Delta t}{2}=1.15\,м$$
На расстоянии $1.15 \, м$ от счетчика $A$