$1.1.5^*.$ Три микрофона, расположенные на одной прямой в точках $A$, $B$, $C$, зарегистрировали последовательно в моменты времени $t_A > t_B > t_c$ звук от взрыва, который произошел в точке $O$, лежащей на отрезке $AC$. Найдите отрезок $AO$, если $AB = BC = L$. В какой момент времени произошел взрыв?
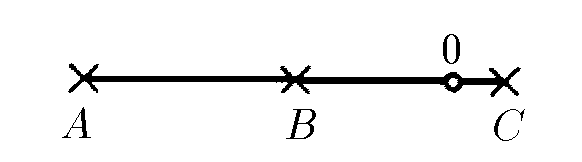
Пусть взрыв произошел в момент времени $t_0$, тогда время регистрации сигнала в точке $A$ равно:
$$t_A = t_0 + \frac{L + x}{c}, \, (1)$$
где $x = BO$. Аналогично для точки $B$
$$t_B = t_0 + \frac{x}{c}, \,(2)$$
Для точки $C$
$$t_C = t_0 + \frac{L - x}{c}, \,(3)$$
Из первого уравнения вычтем второе:
$$t_A – t_B = \frac{L}{c}. \,(4)$$
А из первого уравнения вычтем третье
$$t_A – t_C = \frac{2x}{c}. \,(5)$$
Из $(4)$ уравнения выразим $c = \frac{L}{t_A – t_B}$, а из $(5)$ $x = \frac{t_A – t_C}{2} \cdot c$, Тогда искомое расстояние
$$AO = L + x = L + \frac{t_A – t_C}{2}\frac{L}{t_A – t_B}$$
После преобразования
$$AO = \frac{3t_A – 2t_B – t_C}{2(t_A – t_B)} \cdot L. \, (6)$$
Для определения момента времени в который произошел взрыв, подставим в выражение
$$t_A = t_0 + \frac{L + x}{c}, \; c = \frac{L}{t_A – t_B}$$ $$\frac{t_A – t_C}{2} = \frac{x}{c}$$
после преобразований
$$t_0 = t_B - \frac{1}{2} \cdot (t_A – t_C)$$
$$AO = \frac{3t_A – 2t_B – t_C}{2(t_A – t_B)} \cdot L, \; t_0 = t_B - \frac{1}{2} \cdot (t_A – t_C)$$