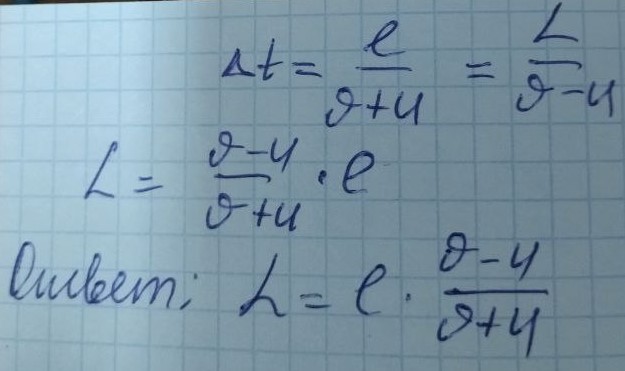$1.1.6.$ Спортсмены бегут колонной длины $l$ со скоростью $v$. Навстречу бежит тренер со скоростью $u < v$. Каждый спортсмен, поравнявшись с тренером, разворачивается и начинает бежать назад с той же по модулю скоростью $v$. Какова будет длина колоны, когда все спортсмены развернуться.
Мысленно остановим колону, тогда тренер кроме своей скорости будет иметь скорость колонны, направленную в противоположную сторону. С этой относительной скоростью $v + u$ он в течение времени
$$t = \frac{l}{v + u}$$
пробежит вдоль колонны и сравняется с хвостом. Голова колоны, развернувшись, будет двигаться с относительной скоростью $v - u$ и через время
$$t = \frac{{l}'}{v - u}$$
где ${l}'$ – длина новой «колоны» после обгона. Тогда
$$\frac{{l}'}{v - u} = \frac{l}{v + u}$$
и длина новой колонны
$$\fbox{${l}' = \frac{v - u}{v + u}l$}$$
Когда все спортсмены развернуться длина новой колоны будет равна ${l}' = \frac{v - u}{v + u}l$