$1.1.9. а.$ Из взрывчатого вещества изготовлен стержень длины $l$. Скорость детонации (скорость вовлечения во взрыв новых участков взрывчатого вещества) равна $v$, а скорость разлета продуктов взрыва $u < v$. Как изменяется со временем область, занятая продуктами взрыва, если стержень подрывается с одного из концов? Сделайте рисунок.
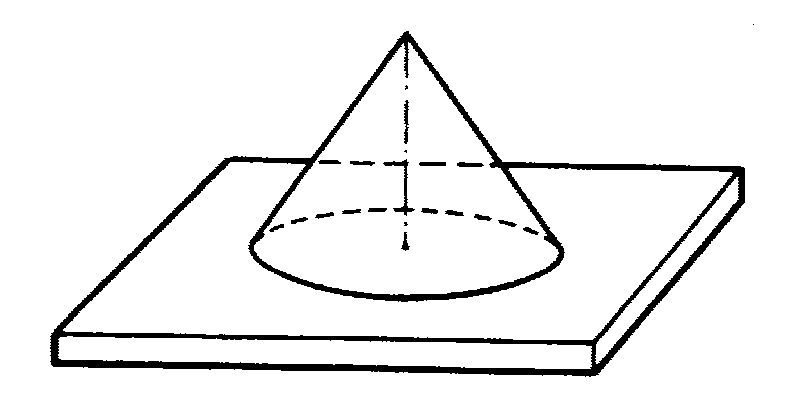
$б^{∗}$. Из этого же взрывчатого вещества нужно изготовить такую тонкостенную коническую оболочку, чтобы при подрыве ее с вершины продукты взрыва одновременно ударили по плите. Какой угол между осью конуса и образующей нужно выбрать?
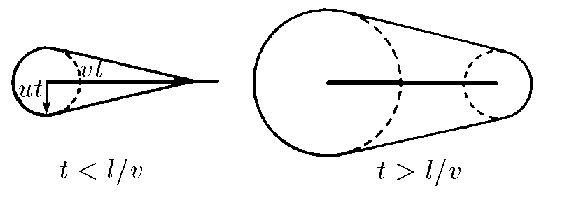
1. Конфигурация области, занятой продуктами взрыва до момента полного окисления стержня, при $\tau < L/v$ будет иметь вид конуса высотой $h = vt$, основанием которого служит полусфера радиуса $R = u \cdot t$.
2. После того, как окисление стержня закончится, т.е. для времени $\tau\geq L/v$ область продуктов будет ограничена двумя полусферами с радиусами
$$R=ut \text{ и }r=u(t-\frac{L}{v})$$
1. Если длина образующей конуса $L$, то его высота $h$ определяется уравнением
$$h = L \cdot \cos\alpha$$
откуда
$$L = \frac{h}{\cos\alpha}$$
2. По условию задачи $t_1=t_2$, т.е.
$${t_{1}=\frac{h}{u}=\frac{L\cos\alpha}{u};\quad t_{2}=\frac{L}{v},}$$
откуда
$$\frac{{L}}{{v}}=\frac{{L}\cos\alpha}{{u}}\quad\Rightarrow\quad\fbox{$\cos\alpha =\frac{{u}}{{v}}$}\quad$$
а. При $t < l/v$ граница области — конус с вершиной, находящейся на расстоянии $vt$ от конца стержня, переходящий в касающуюся его сферу радиуса $ut$. При $t > l/v$ — сферы с центрами на концах стержня и радиусами $ut$ и $u(t − l/v)$ с касательной к ним конической поверхностью. $\\ б^{∗}. \; \cos\alpha = u/v$