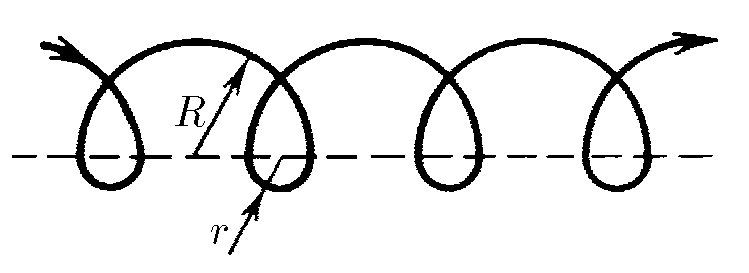
$1.2.1.$ На рисунке изображена траектория электрона, который дрейфует вдоль плоскости раздела областей с различными магнитными полями. Его траектория состоит из чередующихся полуокружностей радиуса $R$ и $r$. Скорость электрона постоянна по модулю и равна $v$; найдите среднюю скорость электрона за большой промежуток времени.
Рассмотрим движение электрона от точки $ A $ до точки $ B $. В этих точках электрон находится в равной «фазе». Последующее движение электрона будет повторяться.
Перемещение электрона вдоль линии раздела областей
$ S = N \cdot (2R - 2r) $.
Затраченное время равно сумме
$$ t = N \cdot \left( \frac{\pi R}{v} + \frac{\pi r}{v} \right) = N \cdot \frac{\pi}{v} \cdot (R + r) $$
Средняя скорость электрона за большой промежуток времени
$$ v_{ср} = \frac{S}{t} = \frac{N \cdot 2(R - r)}{N \cdot \frac{\pi}{v}(R + r)} $$
после преобразования
$$\fbox{$v_{ср} = \frac{2}{\pi} \cdot v \cdot \frac{R - r}{R + r}$}$$