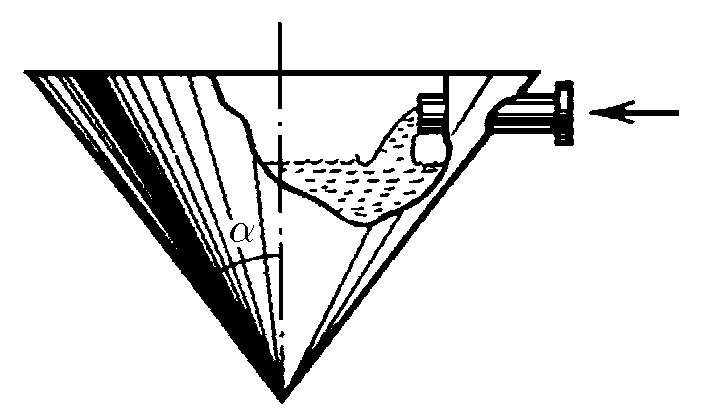
$1.2.11^*.$ $а$. В коническом сосуде уровень воды поднимается с постоянной скоростью $v_0$. Как зависит от времени скорость поступления воды в сосуд через трубку сечения $s$? В нулевой момент времени сосуд пуст.
$б$. Струя масла, попадающая на поверхность воды, растекается по ней круглым пятном толщины $h$. Как зависит от времени скорость движения границы пятна, если в единицу времени поступает объем масла $q$? В начальный момент времени радиус пятна равен нулю.
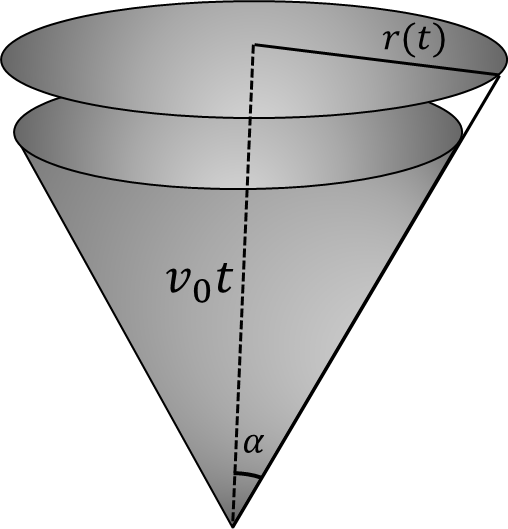
$a)$ К моменту времени $t$, уровень воды будет равен $v_0t$. А скорость изменения объема будет равна:
$$\frac{dV}{dt} = \frac{\pi r(t)^2 dx}{dt}$$
Где $dx$ - изменение уровня воды:
$$\frac{dV}{dt} = \pi r(t)^2 v_0$$
Из геометрии,
$$r(t) = v_0 t \cdot \tan\alpha$$
По определению, скорость поступающей воды равна $v = \frac{dV}{sdt}$
Подставляя предыдущие выражения:
$$v = {\pi v_0^3 t^2 \cdot \tan^2(\alpha )}/s$$
$б)$ За малый промежуток времени $dt$ объем изменяется на $dV = q dt$
Также приращение объема можно расписать как $dV = 2\pi r dr \cdot h $
Таким образом:
$ q dt = 2\pi r dr \cdot h$
Учитывая $v = \frac{dr}{dt}$,
$$ \fbox{$v = \frac{q}{2\pi r h}$}$$
а. $v=\frac{\pi v_0^3t^2\operatorname{tg}^2\alpha}{s}$; б. $v=\frac{1}{2}\sqrt{\frac{q}{\pi ht}}$