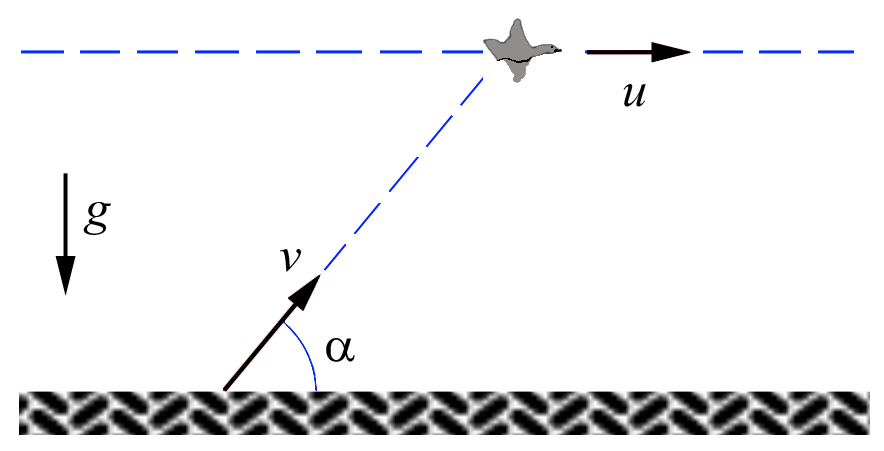
$1.3.10.$ Утка летела по горизонтальной прямой с постоянной скоростью $u$. В нее бросил камень неопытный «охотник»,причем бросок был сделан без упреждения, т.е. в момент броска скорость камня $v$ была направлена как раз на утку под углом $\alpha$ к горизонту. На какой высоте летела утка, если камень всеже попал в нее?
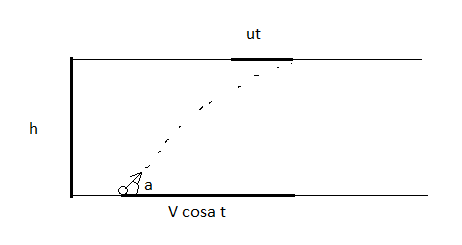
Рассмотрим данное уравнение движения:
$$y = h = \nu\sin\alpha - \frac{gt^{2}}{2}$$
Известно, что:
$\left\{\begin{matrix} S_{yt}=ut \\ S_{o}=\nu t \cos\alpha \end{matrix}\right.$
Для угла $\alpha$:
$$\tan\alpha = \frac{h}{S_{o} - S_{yt}} = \frac{h}{t(\nu\cos\alpha - u)}$$
Подставляем значение угла $\alpha$ в уравнение для высоты:
$$h = t (\nu\cos\alpha - u) \tan\alpha = \nu t \sin\alpha - \frac{gt^{2}}{2}$$
Из этого уравнения можно выразить время $t$:
$$t = \frac{2u \tan\alpha}{g}$$
Подставляем значение времени $t$ обратно в уравнение для высоты:
$$\fbox{$h = \frac{2u \tan^{2} \alpha}{g} (\nu\cos\alpha - u)$}$$