$1.3.11.$ Из отверстия шланга, прикрытого пальцем, бьют две струи под углом $\alpha$ и $\beta$ к горизонту с одинаковой начальной скоростью $v$. На каком расстоянии от отверствия по горизонтали струи пересекутся?
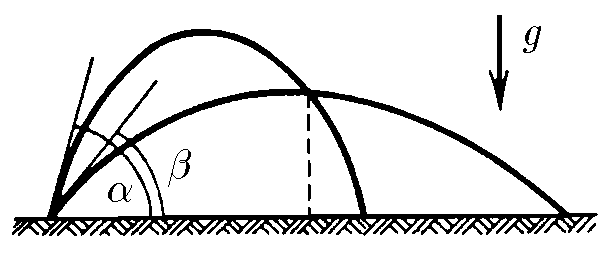
$vt_{1} \cdot \cos\alpha = vt_{2} \cdot \cos\beta$
$$vt_{1}\cdot \sin\alpha - \frac{gt_{1}^{2}}{2}=vt_{2}\cdot \sin\beta -\frac{gt_{2}^{2}}{2}$$
Из первого уравнения,
$$t_{1}=t_{2} \cdot \frac{\cos\beta}{\cos\alpha}$$
Подставляем $t_{1}$ во второе уравнение и выразим $t_{2}$. Пригодятся тригонометрические формулы 63. Уже полученный $t_{2}$ достаточно вставить в $x=vt_{2}\cos\beta$, где $x$ - искомое расстояние.
Используя тригонометрические формулы:
$$t_{2}= \frac{2\nu^{2}}{g(\tan\beta +\tan\alpha )\cos\beta}$$
$$\fbox{$x = \frac{2\nu^{2}}{g(\tan\beta +\tan\alpha )}$}$$