$1.3.16^*.$ В трубу длины $l$, наклоненную под углом $\alpha$ к горизонту, влетает шарик с горизонтальной скоростью $v$. Определите время пребывания шарика в трубе, если удары шарика о ее стенки упругие.
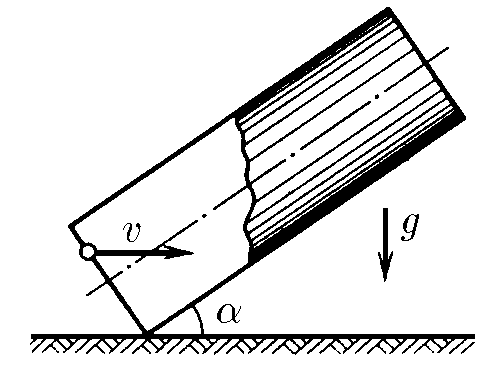
a) Найдем условие, при котором соудареня будут отсутсвовать$(x=0)$
Из закона сохранения энергии:
$$\frac{mv_0^2}{2} = mgl \cdot \sin\alpha$$
$$v_{0}\leq\frac{\sqrt{2gl\sin\alpha}}{\cos\alpha}$$
В этом случае пройдет время
$$ t = \frac{2v_0}{g} \text{ctg} \alpha$$
b) Теперь рассмотрим те случаи, когда происходит касание:
$$v_{0}>\frac{\sqrt{2gl\sin\alpha}}{\cos\alpha}$$
Путь между двумя касаниями:
$$L=v_{0}\cos\alpha t-\frac{g\sin\alpha t^{2}}{2}$$
При получении необходимого времени выбираем именно тот, который меньший, т.к. необходимо найти время когда он выйдет
$$t=\frac{v_{0}\cos\alpha -\sqrt{v_{0}^{2}\cos^{2}\alpha -2g\sin\alpha L}}{g\sin\alpha}$$
$\begin{aligned}&t=\frac{2v}{g}\operatorname{ctg}\alpha\text{ при }v\cos\alpha <\sqrt{2gl\sin\alpha};\&t=\frac vg\operatorname{ctg}\alpha\bigg(1-\sqrt{1-\frac{2gl\operatorname{tg}\alpha}{v^2\cos\alpha}}\bigg)\text{ при }v\cos\alpha >\sqrt{2gl\sin\alpha}.\end{aligned}$