$1.3.22^*.$ Самолеты летят по одной прямой навстречу друг другу с одинаковой скоростью $v$. Предельная дальность обнаружения ими друг друга $l$. Один самолет после обнаружения другого совершает разворот, не меняя модуля скорости, и летит параллельно второму самолету. При каком постоянном ускорении самолеты потеряют друг друга из вида в конце разворота?
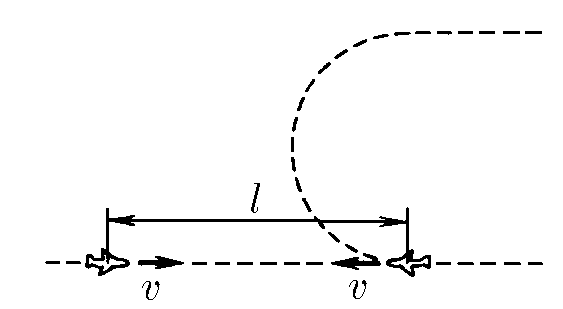
Чтобы самолеты потеряли друг друга необходимо, чтобы к концу разворота расстояние между ними состовляло $l$
По оси $Oy$ - второй самолет сместиться на величину двойного радиуса-кривизны траектории разворота, а первый самолет сместиться за время $t$ на величину $vt$ по оси $Ox$.
Запишем условие потери из виду
$ (2r)^2 + (l-vt)^2 = l^2\quad(1)$
Т.к. скорость остается неизменной $v = \text{сonst}$
$ vt = \pi r\quad(2)$
Подcтавляем $(2)$ в $(1)$
$ (4+\pi^2)r^2 - 2l \pi r = 0\quad(3)$
Выражаем $r$
$$ r = l \frac{2 \pi}{4+\pi^2}\quad(4)$$
Тогда, ускорение, с которым движется второй самолет
$$ a = \frac{v^2}{r} = \frac{v^2}{l} \frac{4+\pi^2}{2 \pi}\quad(5)$$