$1.3.3^*.$ Под каким углом к вертикали должен быть направлен из точки $A$ гладкий желоб, чтобы шарик соскользнул по нему на наклонную плоскость за наименьшее время?
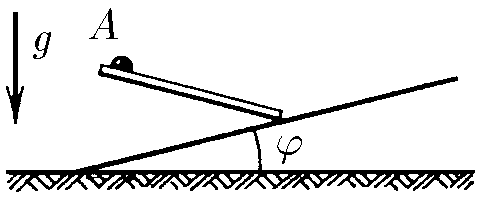
Рассмотрим возможные направления желоба из точки $A$. Видно, что меняя угол наклона желоба к плоскости меняется и длина желоба, но также изменяется и ускорение с которым шарик будет двигаться по желобу.
Из геометрических соображений:
$h = x \cdot \tan{\alpha} + x \cdot \tan{\varphi}$;
$$l = \frac{x}{\cos{\alpha}}\; (1)$$
Шарик будет скатываться с ускорением:
$a = g \cdot \sin{\alpha}$.
Время находим из условия, что шарик прошёл путь $l$:
$$l = \frac{a t^2}{2}$$
$$\frac{x}{\cos{\alpha}} = \frac{g \cdot \sin{\alpha} \cdot t^2}{2}$$
Следовательно, выражая из $(1)$ $x$, получаем из последнего уравнения:
$$t^2 = \frac{2h}{g \cdot \sin{\alpha} \cdot \cos{\alpha} (\tan{\alpha} + \tan{\varphi})}$$
Время будет минимальным, если $\xi =g \cdot \sin{\alpha} \cdot \cos{\alpha} (\tan{\alpha} + \tan{\varphi})$ будет максимальным.
$$\xi = \frac{\sin{\alpha}}{\cos{\varphi}} \sin{(\alpha + \varphi)} $$
$$\xi = \frac{1}{2 \cos{\varphi}} (\cos{\varphi} - \cos{(2\alpha + \varphi)})$$
Это выражение будет максимальным, когда $\cos{(2\alpha + \varphi)}$ будет минимальным, а значит равно $-1$. Тогда $2\alpha + \varphi = \pi$, откуда:
$$\alpha = \frac{\pi}{2} - \frac{\varphi}{2}$$
Угол желоба к вертикали равен:
$$\beta = \frac{\pi}{2} - \alpha$$
$$\fbox{$\beta =\frac{\varphi}{2}$}$$