$1.3.7.$ По гладкой наклонной плоскости со скоростью $v$ пускают шарик. Какое расстояние по горизонтали он пройдет, прежде чем скатится с плоскости? Плоскость наклонена к горизонту под углом $45^{\circ}$. Начальная скорость шарика образует угол $45^{\circ}$ с горизонтальным краем плоскости падения на Земле?
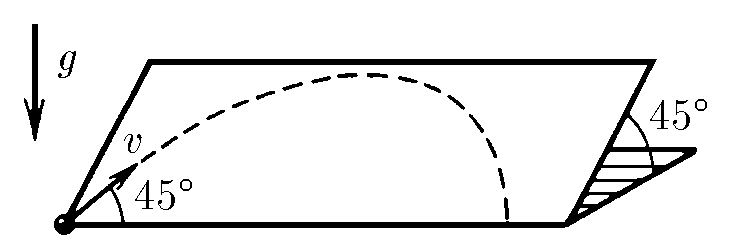
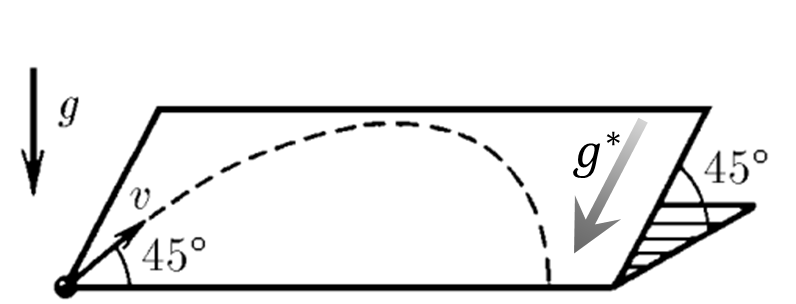
На наклонной плоскости на тело действует компонента ускорения свободного падения:
$a = g^* = g \cdot \cos{45^{\circ}}$
Из формулы для дальности полета, полученной в 1.3.6 следует:
$$L=\frac{v^2}{g^*}\operatorname{sin}90^{\circ}$$
Подставляем $g^*$:
$$\fbox{$L=\frac{v^2 \sqrt{2}}{g}$}$$