$1.3.8.$ Из миномета ведут стрельбу по объектам, расположенным на склоне горы. На каком расстоянии от миномета будут падать мины, если их начальная скорость $v$, угол наклона горы $\alpha$ и угол стрельбы по отношению к горизонту $\beta$?
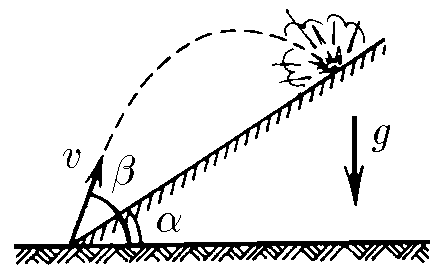
Уравнения движения снаряда могут быть записаны следующим образом:
${x}={v}_{0}{t}\cos{\beta}$
$${y}={v}_{0}{t}\sin{\beta}-\frac{{g}{t}^{2}}{2}$$
Подставим в уравнения координаты цели $x = L; \;y = L \tan\alpha$
${L=v_{0}t\cos\beta}$
$$L\tan\alpha =v_{0}t\sin\beta -\frac{gt^{2}}{2}$$
Выразим из первого уравнения последней системы уравнений время и подставим его значение во второе уравнение
$${t=\frac{L}{v_{0}\cos\beta}}$$
$${L\tan\alpha =v_{0}\frac{L}{v_{0}\cos\beta}\sin\beta -\frac{g}{2}\frac{L^{2}}{v_{0}^{2}\cos^{2}\beta} }$$
Откуда
$${v}_{0}=\sqrt{\frac{{gL}\cos\alpha}{2\cos\beta\sin(\beta -\alpha )}}$$
Выражаем $L$,
$$L = \frac{ 2\cos\beta\sin(\beta -\alpha )\cdot v^2_0}{g\cos\alpha}$$
И находим дальность полета вдоль стенки:
$$l = \frac{L}{\cos\alpha} $$
$$\fbox{$l = \frac{ 2v^2_0}{g} \frac{ \cos\beta\sin(\beta -\alpha )}{\cos^2 \alpha}$}$$