$1.4.13.$ Шестеренка радиуса $R$ помещена между двумя параллельными зубчатыми рейками. Рейки движутся со скоростью $v_1$ и $v_2$ навстречу друг другу. Какова частота вращения шестеренки?
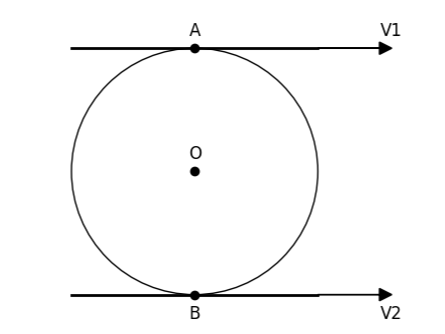
Перейдем в СО центра диска. В этой СО скорость верхней и нижней точек диска одинакова по модулю и противоположны по направлению. Поэтому
$(v_{1} - v) = - (v_{2} - v)$
Откуда
$$v = \frac{v_{1} + v_{2}}{2}$$
Частоту вращения найдем как
$$\nu = \frac{v}{R}$$
Подставляем $v$
$$\fbox{$\nu = \frac{v_1 + v_2}{2R}$}$$