$1.4.15^*.$ Имеется пучок одинаковых ядер, движущихся со скоростью $v$. Ядра в пучке самопроизвольно делятся на пары одинаковых осколков. Скорость осколков, движущихся в направлении пучка, равна $3v$. Найдите скорость осколков, движущихся в направлении, перпендикулярном пучку.
Перейдем в СО центра масс пучка.
В этой системе отсчета относительная скорость связана со скоростью в НСО соотношением
$ \vec{v'} = \vec{v} + \vec{v}_{отн} $
Где $\vec{v'}$ и $\vec{v}$ - скорость в НСО и скорость ЦМ системы, соответственно.
По условию, когда $\vec{v}_{отн}$ и $\vec{v}$ сонаправлены $v' = 3 v$

Откуда
$v_{отн} = 2v$
Далее рассмотрим осколки, которые полетели со скоростью $\vec{v}_\perp$)
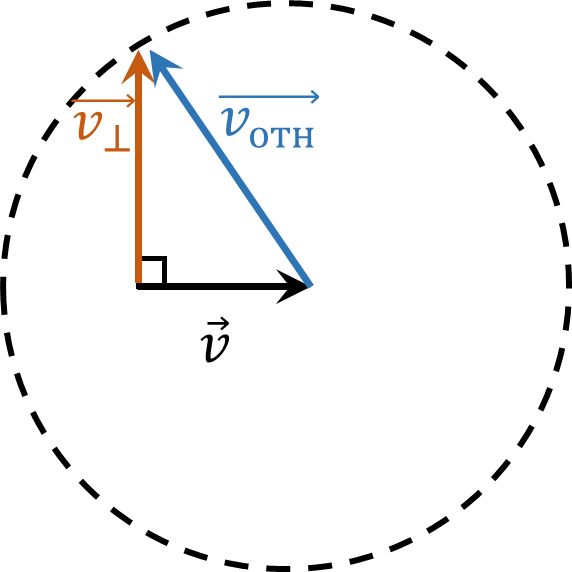
Переходя обратно в НСО, получаем, что
$\vec{v}_\perp = \vec{v}_{отн}-\vec{v}$
По теореме Пифагора
$\fbox{${v}_\perp = 3{v}$}$