$1.4.5. а.$ Капли дождя из-за сопротивления воздуха падают с постоянной скоростью $v$, перпендикулярной поверхности земли. Как необходимо расположить цилиндрическое ведро, находящееся на движущейся со скоростью $u$ платформе, чтобы капли не попадали на его стенки?
$б.$ При скорости ветра $v = 10 \,м/с$ капли дождя падают под углом $\beta = 30^{\circ}$ к вертикали. При какой скорости ветра капли будут падать под углом $\beta = 45^{\circ}$?
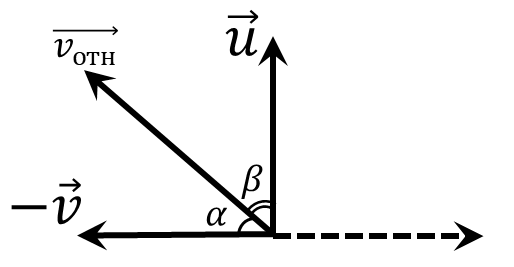
а) Чтобы капли дождя не попадали на стенки ведра необходимо, чтобы их относительная скорость была параллельна стенкам ведра.
В ИСО связанной с каплями дождя, угол $\alpha$ между относительной скоростью и горизонтальную определяется как
$\tan\varphi = u/v \; (1)$
Под этим же углом должны и находится стенки ведра.
б) Учитывая, связь угла с вертикалью и горизонталью $\beta = 90^{\circ} - \alpha$. Подставляем численные данные в $(1)$ и решаем систему:
$\left\{\begin{matrix} 10 \cdot \tan 60^{\circ} = u\\ v \cdot \tan 45^{\circ} = u \end{matrix}\right.$
$а.$ Ведро должно быть наклонено в сторону движения платформы под углом $\varphi$ к вертикали: $\tan\varphi = u/v.$
$б.$ $u = 10\sqrt{3} \, м/с.$